Question

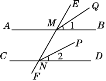
【题目】如图，在10×10的正方形网格中（每个小正方形的边长都为1个单位），△ABC的三个顶点都在格点上．建立如图所示的直角坐标系，

（1）请在图中标出△ABC的外接圆的圆心P的位置，并填写： 圆心P的坐标：P（ , ）
（2）将△ABC绕点A逆时针旋转90°得到△ADE，画出图形，并求△ABC扫过的图形的面积．

Answer 1

【答案】
（1）5,3
（2）解：根据图中信息由勾股定理可得： ，∴△ABC在旋转过程中扫过的面积为：S扇形ACE+S△ABC= .

【解析】（1）三角形外接圆的圆心是三边垂直平分线的交点，因此作出边AB、BC的垂直平分线的交点，即可求出点P的坐标。
（2）根据旋转的性质，注意旋转的方向和旋转的角度画出旋转后的图形；观察图形可知，△ABC扫过的图形的面积=S扇形ACE+S△ABC，根据勾股定理求出AC的长后，即可算出结果。
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对三角形的外接圆与外心的理解，了解过三角形的三个顶点的圆叫做三角形的外接圆，其圆心叫做三角形的外心．