题目内容
【题目】如图①,长方形ABCD中,AB=8,BC=10,在边CD上取一点E,将△ADE折叠后点D恰好落在BC边上的点F.
(1)求CE的长;
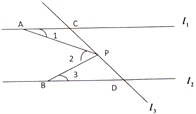
(2)建立平面直角坐标系如图②所示,在x轴上找一点P,使PA+PE的值最小,求出最小值和点P的坐标;
(3)如图③,DE的延长线与AF的延长线交于点G,在y轴上是否存在点M,使△FGM是直角三角形?如果存在,求出点M的坐标:如果不存在,说明理由.

【答案】(1)3(2)P(![]() ,0),最小值为
,0),最小值为![]() (3)存在;M坐标为(0,﹣
(3)存在;M坐标为(0,﹣![]() )或(0,﹣4.5)
)或(0,﹣4.5)
【解析】
(1)设CE=x,知DE=EF=8﹣x,由AD=AF=10,AB=8知BF=6,CF=4,根据CE2+CF2=EF2求解可得.
(2)作点E关于x轴的对称点Q,连接AQ,与x轴的交点即为所求,先得出DQ的长度,再根据AQ=![]() 可得最小值;再求出直线AQ解析式为y=﹣
可得最小值;再求出直线AQ解析式为y=﹣![]() x+8,据此进一步求解可得.
x+8,据此进一步求解可得.
(3)先证△AOF∽△GCF得![]() ,据此求得G(10,﹣
,据此求得G(10,﹣![]() ),根据点M(0,a),F(6,0)知MF2=a2+36,GM2=102+(a+
),根据点M(0,a),F(6,0)知MF2=a2+36,GM2=102+(a+![]() )2,FG2=16+(
)2,FG2=16+(![]() )2,分MF2+GM2=FG2,FG2+GM2=MF2,FG2+MF2=GM2三种情况分别求解可得.
)2,分MF2+GM2=FG2,FG2+GM2=MF2,FG2+MF2=GM2三种情况分别求解可得.
(1)如图①,

设CE=x,
则DE=EF=8﹣x,
∵AD=AF=10,AB=8,
∴BF=6,
∴CF=4,
在Rt△CEF中,由CE2+CF2=EF2得x2+42=(8﹣x)2,
解得x=3,即CE=3;
(2)如图②,作点E关于x轴的对称点Q,连接AQ,与x轴的交点即为所求.

则CE=CQ=3,
∴点Q(10,﹣3),
∴DQ=CD+CQ=11,
∴AQ=![]() =
=![]() =
=![]() ,
,
由A(0,8),Q(10,﹣3)可得直线AQ解析式为y=﹣![]() x+8,
x+8,
当y=0时,﹣![]() x+8=0,
x+8=0,
解得:x=![]() ,
,
所以点P(![]() ,0),最小值为
,0),最小值为![]() ;
;
(3)如图③,设M(0,a),

∵∠AOF=∠GCF=90°,∠AFO=∠GFC,
∴△AOF∽△GCF,
∴![]() ,即
,即![]() ,
,
解得GC=![]() ,
,
则G(10,﹣![]() ),
),
∵F(6,0),
∴MF2=62+a2=a2+36,GM2=102+(a+![]() )2,FG2=(10﹣6)2+(﹣
)2,FG2=(10﹣6)2+(﹣![]() ﹣0)2=16+(
﹣0)2=16+(![]() )2,
)2,
①若MF2+GM2=FG2,即a2+36+102+(a+![]() )2=16+(
)2=16+(![]() )2,
)2,
整理,得:3a2+16a+180=0,
此方程无解;
②若FG2+GM2=MF2,即16+(![]() )2+102+(a+
)2+102+(a+![]() )2=a2+36,
)2=a2+36,
解得a=﹣![]() ,则M(0,﹣
,则M(0,﹣![]() );
);
③若FG2+MF2=GM2,即16+(![]() )2+a2+36=102+(a+
)2+a2+36=102+(a+![]() )2,
)2,
解得a=﹣4.5,则M(0,﹣4.5);
综上,点M的坐标为(0,﹣![]() )或(0,﹣4.5).
)或(0,﹣4.5).

 名校课堂系列答案
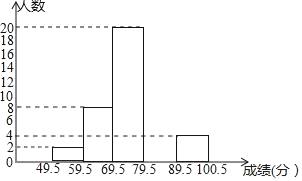
名校课堂系列答案【题目】某校数学兴趣小组成员刘明对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析(每个人的成绩各不相同),绘制成如下下频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题:
(1)频数、频率分布表中a= ,b= ,c= ;
(2)补全频数分布直方图;
(3)如果要画该班上学期期末考试数学成绩的扇形统计图,那么分数在69.5﹣79.5之间的扇形圆心角的度数是 ;
(4)张亮同学成绩为79分,他说:“我们班上比我成绩高的人还有![]() ,我要继续努力.”他的说法正确吗?请说明理由.
,我要继续努力.”他的说法正确吗?请说明理由.
分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
频数 | 2 | 8 | 20 | a | 4 | c |
频率 | 0.04 | b | 0.40 | 0.32 | 0.08 | 1 |