题目内容
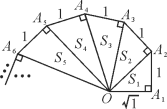
【题目】如图所示的是用棋子成的T字形图案:
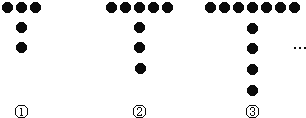
(1)填写下表:
图案序号 | ① | ② | ③ | ④ | …… | ⑧ |
每个图案中棋子的个数 | 5 | 8 | …… |
(2)第![]() 个“T“字形图案中棋子的个数为多少 (用含
个“T“字形图案中棋子的个数为多少 (用含![]() 的代数式表示);
的代数式表示);
(3)第20个“T”字形图案共有棋子多少个?
(4)计算前20个“T”字形图案中棋子的总个数.
【答案】(1)11,14,26 (2)3n+2 (3)62 (4)670
【解析】
(1)通过观察已知图形可得:每个图形都比其前一个图形多3枚棋子,得出摆成第③④⑧个图形需要的棋子数;
(2)由(1)得出规律为摆成第n个图形需要(3n+2)个棋子;
(3)将n=20代入(2)中规律计算即可求解;
(4)由(2)中规律求解即可.
解:(1)首先观察图形,得到前面三个图形的具体个数,不难发现:在5的基础上依次多3枚.即第n个图案需要5+3(n-1)=3n+2.那么当n=3时,则有11枚;当n=4时,则有14枚;当n=8时,则有26枚;
填表如下:
图形序号 | ① | ② | ③ | ④ | … | ⑧ |
每个图案中棋子个数 | 5 | 8 | 11 | 14 | … | 26 |
(2)因为第①个图案有5枚棋子,
第②个图案有(5+3×1)枚棋子,
第③个图案有(5+3×2)枚棋子,
依此规律可得第n个图案需5+3×(n-1)=5+3n-3=(3n+2)枚棋子.
(3)第20个“T”字形图案共有棋子3×20+2=62(个).
即第20个图案需62个棋子;
(4)前20个“T”字形图案中棋子的总个数为:
5+8+11+14+17+…+53+56+59+62
=(5+62)+(8+59)+(11+56)+…+(32+35)
=67×10
=670(个).

练习册系列答案
相关题目