Question

【题目】旋转变换是全等变换的一种形式，我们在解题实践中经常用旋转变换的方法来构造全等三角形来解决问题。

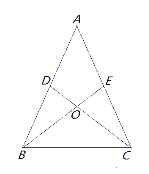
（1）方法探究：如图①，在△ABC中，∠BAC=90°，AB=AC，点D、E在边BC上，∠DAE=45°

试探究线段BD、CE、DE可以组成什么样的三角形。我们可以过点B作BF⊥BC，使BF=EC，连接AF、DF，易得∠AFB=45°进而得到△AFB≌△AEC，相当于把△AEC绕点A顺时针旋转90°到△AFB，请接着完成下面的推理过程：

∵△AFB≌△AEC，

∴∠BAF= ，AF=AE，

∵∠BAC=90°，∠DAE=45°，

∴∠BAD+∠CAE= ，

∴∠BAF+∠BAD=45°，

∴∠DAF=45°= ，

在△DAF与△DAE中，

AF=AE，

∠DAF=∠DAE，

AD=AD，

∴△DAF≌△DAE，

∴DF= ，

∵BD、BF、DF组成直角三角形，

∴BD、CE、DE组成直角三角形.

（2）方法运用

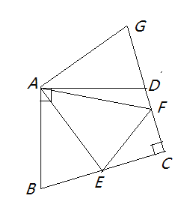
① 如图②，在四边形ABCD中，AB=AD，∠BAD=∠BCD=90°，∠ABC+∠ADC=180°，点E在边BC上，点F在边CD上，∠EAF=45°试判断线段BE、DF、EF之间的数量关系，并说明理由。

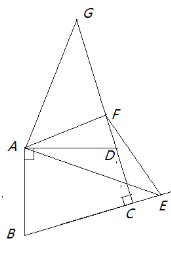
② 如图③，在①的基础上若点E、F分别在BC和CD的延长线，其他条件不变，①中的关系在图③中是否仍然成立？若成立请说明理由；若不成立请写出新的关系，并说明理由。

Answer 1

【答案】（1）∠CAE ， 45°，∠DAE ， DE ；（2）①EF=BE+DF；②①中关系不成立,EF=BE-DF.

【解析】

(1) 作AF⊥AB，使AF=BE，连接DF，根据SAS证得△CAF≌△CBE和△CDF≌△CDE，再由勾股定理和等量代换即可解答；

(2) 延长CD到G，使DG=BE，证得△ABE≌△ADG,可得AE=AG，∠EAB=∠DAG,可得∠EAF=∠GAF,进而可得△AEF≌△AGF,所以得GF=EF得到EF=BE+DF;

(3) 延长CD到G，使DG=BE，证得△ABE≌△ADG,可得AE=AG，∠DAG=∠EAB=90°-∠DAE,进而可得△AEF≌△AGF,所以得GF=EF,EF=BE-DF .

（1）∠CAE ， 45°，∠DAE ， DE ；

（2）①EF=BE+D.

理由：

延长CD到G，使DG=BE，

则∠ADG+∠ADC=180°，

∵∠ABC+∠ADC=180°

∴∠ABC=∠ADG，

在△ABE和△ADG中，

DG=BE

∠ABC=∠ADG

AB=AD

∴△ABE≌△ADG（SAS），

∴AE=AG，∠EAB=∠DAG,

∴∠EAF=∠GAF=45°,

∴△AEF≌△AGF,

∴GF=EF.

②.①中关系不成立,EF=BE-DF.

理由:

延长CD到G，使DG=BE，

证得△ABE≌△ADG,

可得AE=AG，∠DAG=∠EAB=90°-∠DAE,

∵∠DAF=45°-∠DAE,

∴∠GAF=∠DAG-∠DAF=（90°-∠DAE）-（45°-∠DAE）=45°=∠EAF,

∴△AEF≌△AGF,

∴GF=EF,

∵GF=DG-DF,

∴EF=BE-DF .