题目内容
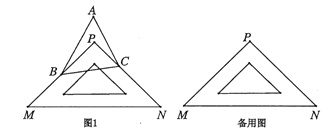
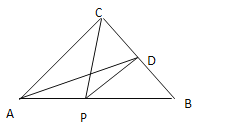
【题目】如图,等腰直角![]() 中,
中,![]() ,
,![]()
![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() 为
为![]() 上的一个动点,当
上的一个动点,当![]() 点运动时,
点运动时,![]() 的最小值为____
的最小值为____
【答案】4
【解析】
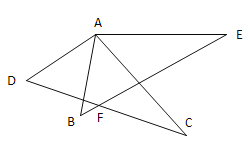
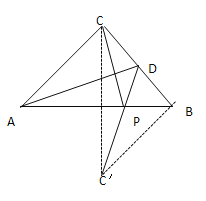
作点C关于AB的对称点C′,连接DC′、BC′,连接DC′交AB于点P,由轴对称的性质易得EC=EC′,则线段DC′的长度即为PC+PD的最小值, 由等腰直角三角形的性质易得∠CBC′=∠CBA+∠C′BA=90![]() ,在Rt△DBC′中,利用勾股定理即可求得线段DC′的长度,问题便可得以解决.
,在Rt△DBC′中,利用勾股定理即可求得线段DC′的长度,问题便可得以解决.
∵![]() ,
,![]()
![]() 为
为![]() 的中点,
的中点,![]() ,
,
∴设CD=x,则AC=2x,
∴x2+(2x)2=42
解得x=![]() ,
,
∴BD=CD=![]() ,BC=AC=
,BC=AC=![]()
如图所示,作点C关于AB的对称点C′,连接DC′、BC′,连接DC′交AB于点E.
∵点C和点C′关于AB对称,
∴PC=PC′,∠CBA=∠C′BA,
∴PC+PD=PC′+PD=DC′,此时PC+PD的长最小.
∵△ABC是等腰直角三角形,AC=BC,
∴∠CBC′=∠CBA+∠C′BA=45![]() +45
+45![]() =90
=90![]() .
.
∴在Rt△DBC′中,由勾股定理得DC′= ![]() =
=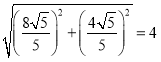 ,
,
∴PC+PD的最小值为4.
故答案为:4.

练习册系列答案
相关题目
【题目】某数学课外活动小组在做气体压强实验时,获得压强p(Pa)与体积V(cm3)之间有下列对应数据:
p(Pa) | … | 1 | 2 | 3 | 4 | 5 | … |
V(cm3) | … | 6 | 3 | 2 | 1.5 | 1.2 | … |
根据表中提供的信息,回答下列问题:
(1)猜想p与V之间的关系,并求出函数关系式;
(2)当气体的体积是12cm3时,压强是多少?