��Ŀ����
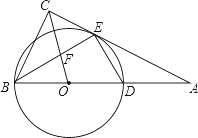
����Ŀ�������龰����ͼ1����ͬһƽ���ڣ���![]() �͵�
�͵�![]() �ֱ�λ��һ��ֱ�����ǰ�
�ֱ�λ��һ��ֱ�����ǰ�![]() ������ֱ�DZ�
������ֱ�DZ�![]() ��
��![]() �ϣ���
�ϣ���![]() ���
���![]() ��ֱ��
��ֱ��![]() ��ͬ�࣬����
��ͬ�࣬����![]() ��
��![]() �ڲ�������
�ڲ�������![]() ��
��![]() ��
��![]() �Ĵ�С�Ƿ�����ij��ȷ����������ϵ��
�Ĵ�С�Ƿ�����ij��ȷ����������ϵ��
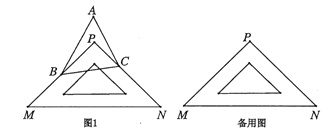
��1������̽������![]() ����
����![]() _________�ȣ�
_________�ȣ�![]() ________�ȣ�
________�ȣ�![]() _________�ȣ�
_________�ȣ�
��2�����̽���������![]() ��
��![]() �Ĺ�ϵ����˵�����ɣ�
�Ĺ�ϵ����˵�����ɣ�
��3��������죺�ı��![]() ��λ�ã�ʹ��
��λ�ã�ʹ��![]() ��
��![]() �⣬�������������䣬�жϣ�2���еĽ����Ƿ���Ȼ����������������˵�����ɣ�������������ֱ��д��
�⣬�������������䣬�жϣ�2���еĽ����Ƿ���Ȼ����������������˵�����ɣ�������������ֱ��д��![]() ��
��![]() ��
��![]() �����������ϵʽ��
�����������ϵʽ��
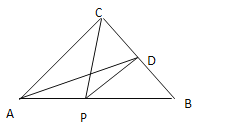
���𰸡���1��125��90��35����2����ABP+��ACP=90��-��A��֤������������3�����۲���������ABP-��ACP=90��-��A����ABP+��ACP=��A-90�����ACP - ��ABP =90��-��A��
��������
��1�������������ڽǺͼ��ɵó���ABC+��ACB����PBC+��PCB��Ȼ�ɵó���ABP+��ACP��
��2�������������ڽǺͶ������е���ת�������ɵó���ABP+��ACP=90��-��A��
��3�����գ�2����ͬ���ķ������е���ת������⼴���ж�.
��1����ABC+��ACB=180��-��A=180��-55��=125�ȣ���PBC+��PCB=180��-��P=180��-90��=90�ȣ�
��ABP+��ACP=��ABC+��ACB -����PBC+��PCB��=125��-90��=35�ȣ�
��2�����룺��ABP+��ACP=90��-��A��
֤��������ABC�У���ABC+��ACB��180��-��A��
�ߡ�ABC=��ABP+��PBC����ACB=��ACP+��PCB��
�ࣨ��ABP+��PBC��+����ACP+��PCB��=180��-��A��
�ࣨ��ABP+��ACP��+����PBC+��PCB��=180��-��A��
�֡���Rt��PBC�У���P=90����
���PBC+��PCB=90����
�ࣨ��ABP+��ACP��+90��=180��-��A��
���ABP+��ACP=90��-��A��
��3���жϣ���2���еĽ��۲�������
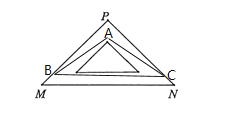
֤��������ABC�У���ABC+��ACB��180��-��A��
�ߡ�ABC=��PBC-��ABP����ACB=��PCB-��ACP��
�ࣨ��PBC+��PCB��-����ABP+��ACP��=180��-��A��
�֡���Rt��PBC�У���P=90����
���PBC+��PCB=90����
���ABP-��ACP=90��-��A����ABP+��ACP=��A-90��
���ACP - ��ABP =90��-��A��

 Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д� �����ÿ�ʱѵ��ϵ�д�
�����ÿ�ʱѵ��ϵ�д� ��Ԫȫ��������ϵ�д�
��Ԫȫ��������ϵ�д� �»ƸԱ����ܾ�ϵ�д�
�»ƸԱ����ܾ�ϵ�д�