Question

【题目】（1）如图1，求证：

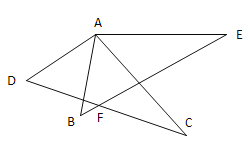
（ 图1）

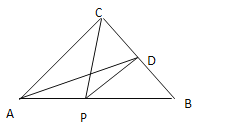
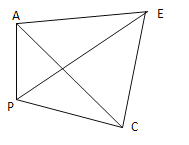
（2）如图2，是等边三角形，为三角形外一点，，求证：

（ 图2）

Answer 1

【答案】（1）见解析（2）见解析

【解析】

（1）根据题意证明△ABE≌△ADC即可求解；

（2）延长CP至B，使PB=PA，连接AB，证△APB为等边三角形得AP=PB=AB，再证△△BAC≌△PAE得EP=BC，可得.

（1）

∴

即

又，

∴△ABE≌△ADC

∴

(2)如图，延长CP至B，使PB=PA，连接AB，

∵

∴∠APB=60，又PB=PA，

∴△APB为等边三角形，

∴AP=PB=AB,∠BAP=60，

∵是等边三角形，

∴AC=AE,∠EAC=60，

∴∠BAP =∠EAC，

∴∠BAP +∠PAC=∠EAC +∠PAC，

即：∠BAC=∠PAE，

在△BAC和△PAE中，

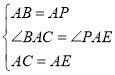
∴△BAC≌△PAE (SAS)，

∴BC=PE，

∵BC=BP+PC=AP+ PC，

∴.