题目内容
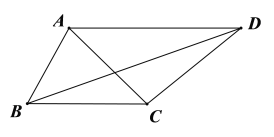
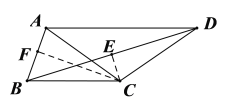
【题目】如图，在四边形
中，
，对角线
平分
，连接
，
，若
，
，则
_________________．
【答案】10
【解析】
由等腰三角形的性质和角平分线的性质可推出AD∥BC，然后根据平行线的性质和已知条件可推出CA=CD，可得CB=CA=CD，过点C作CE⊥BD于点E，CF⊥AB于点F，如图，根据等腰三角形的性质和已知条件可得DE的长和
，然后即可根据AAS证明△BCF≌△CDE，可得CF=DE，再根据三角形的面积公式计算即得结果．
解：∵
，∴∠CBD=∠CDB，
∵
平分
，∴∠ADB=∠CDB，
∴∠CBD=∠ADB，∴AD∥BC，∴∠CAD=∠ACB，
∵
，
，∠CBD=∠CDB，
∴
，∴
，
∴CA=CD，∴CB=CA=CD，
过点C作CE⊥BD于点E，CF⊥AB于点F，如图，则
，
，
∵
，，∴，
在△BCF和△CDE中，∵，∠BFC=∠CED=90°，CB=CD，
∴△BCF≌△CDE（AAS），∴CF=DE=5，
∴
．
故答案为：10．
练习册系列答案
相关题目
