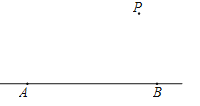题目内容
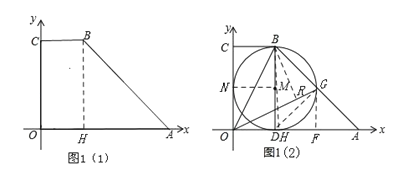
【题目】如图1,直角梯形OABC中,BC∥OA,OA=6,BC=2,∠BAO=45°.
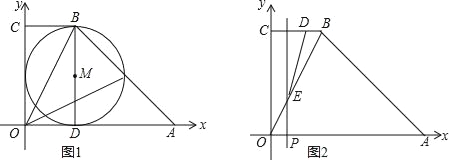
(1)OC的长为 ;
(2)D是OA上一点,以BD为直径作⊙M,⊙M交AB于点Q.当⊙M与y轴相切时,sin∠BOQ= ;
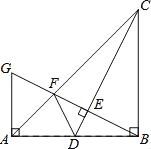
(3)如图2,动点P以每秒1个单位长度的速度,从点O沿线段OA向点A运动;同时动点D以相同的速度,从点B沿折线B﹣C﹣O向点O运动.当点P到达点A时,两点同时停止运动.过点P作直线PE∥OC,与折线O﹣B﹣A交于点E.设点P运动的时间为t(秒).求当以B、D、E为顶点的三角形是直角三角形时点E的坐标.
【答案】(1)4;(2)![]() ;(3)点E的坐标为(1,2)、(
;(3)点E的坐标为(1,2)、(![]() ,
,![]() )、(4,2).
)、(4,2).
【解析】分析:(1)过点B作BH⊥OA于H,如图1(1),易证四边形OCBH是矩形,从而有OC=BH,只需在△AHB中运用三角函数求出BH即可.
(2)过点B作BH⊥OA于H,过点G作GF⊥OA于F,过点B作BR⊥OG于R,连接MN、DG,如图1(2),则有OH=2,BH=4,MN⊥OC.设圆的半径为r,则MN=MB=MD=r.在Rt△BHD中运用勾股定理可求出r=2,从而得到点D与点H重合.易证△AFG∽△ADB,从而可求出AF、GF、OF、OG、OB、AB、BG.设OR=x,利用BR2=OB2﹣OR2=BG2﹣RG2可求出x,进而可求出BR.在Rt△ORB中运用三角函数就可解决问题.
(3)由于△BDE的直角不确定,故需分情况讨论,可分三种情况(①∠BDE=90°,②∠BED=90°,③∠DBE=90°)讨论,然后运用相似三角形的性质及三角函数等知识建立关于t的方程就可解决问题.
详解:(1)过点B作BH⊥OA于H,如图1(1),则有∠BHA=90°=∠COA,∴OC∥BH.
∵BC∥OA,∴四边形OCBH是矩形,∴OC=BH,BC=OH.
∵OA=6,BC=2,∴AH=0A﹣OH=OA﹣BC=6﹣2=4.
∵∠BHA=90°,∠BAO=45°,
∴tan∠BAH=![]() =1,∴BH=HA=4,∴OC=BH=4.
=1,∴BH=HA=4,∴OC=BH=4.
故答案为:4.
(2)过点B作BH⊥OA于H,过点G作GF⊥OA于F,过点B作BR⊥OG于R,连接MN、DG,如图1(2).
由(1)得:OH=2,BH=4.
∵OC与⊙M相切于N,∴MN⊥OC.
设圆的半径为r,则MN=MB=MD=r.
∵BC⊥OC,OA⊥OC,∴BC∥MN∥OA.
∵BM=DM,∴CN=ON,∴MN=![]() (BC+OD),∴OD=2r﹣2,∴DH=
(BC+OD),∴OD=2r﹣2,∴DH=![]() =
=![]() .
.
在Rt△BHD中,∵∠BHD=90°,∴BD2=BH2+DH2,∴(2r)2=42+(2r﹣4)2.
解得:r=2,∴DH=0,即点D与点H重合,∴BD⊥0A,BD=AD.
∵BD是⊙M的直径,∴∠BGD=90°,即DG⊥AB,∴BG=AG.
∵GF⊥OA,BD⊥OA,∴GF∥BD,∴△AFG∽△ADB,
∴![]() =
=![]() =
=![]() =
=![]() ,∴AF=
,∴AF=![]() AD=2,GF=
AD=2,GF=![]() BD=2,∴OF=4,
BD=2,∴OF=4,
∴OG=![]() =
=![]() =2
=2![]() .
.
同理可得:OB=2![]() ,AB=4
,AB=4![]() ,∴BG=
,∴BG=![]() AB=2
AB=2![]() .
.
设OR=x,则RG=2![]() ﹣x.
﹣x.
∵BR⊥OG,∴∠BRO=∠BRG=90°,∴BR2=OB2﹣OR2=BG2﹣RG2,
∴(2![]() )2﹣x2=(2
)2﹣x2=(2![]() )2﹣(2
)2﹣(2![]() ﹣x)2.
﹣x)2.
解得:x=![]() ,∴BR2=OB2﹣OR2=(2
,∴BR2=OB2﹣OR2=(2![]() )2﹣(
)2﹣(![]() )2=
)2=![]() ,∴BR=
,∴BR=![]() .
.
在Rt△ORB中,sin∠BOR=![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.
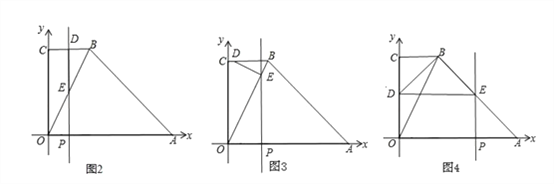
(3)①当∠BDE=90°时,点D在直线PE上,如图2.
此时DP=OC=4,BD+OP=BD+CD=BC=2,BD=t,OP=t. 则有2t=2.
解得:t=1.则OP=CD=DB=1.
∵DE∥OC,∴△BDE∽△BCO,∴![]() =
=![]() =
=![]() ,∴DE=2,∴EP=2,
,∴DE=2,∴EP=2,
∴点E的坐标为(1,2).
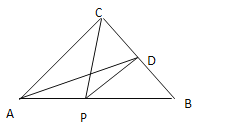
②当∠BED=90°时,如图3.
∵∠DBE=OBC,∠DEB=∠BCO=90°,∴△DBE∽△OBC,
∴![]() =
=![]() =
=![]() ,∴BE=
,∴BE=![]() t.
t.
∵PE∥OC,∴∠OEP=∠BOC.
∵∠OPE=∠BCO=90°,∴△OPE∽△BCO,
∴![]() =
=![]() =
=![]()
![]() t.
t.
∵OE+BE=OB=2![]() t+
t+![]() t=2
t=2![]() .
.
解得:t=![]() ,∴OP=
,∴OP=![]() ,OE=
,OE=![]() ,∴PE=
,∴PE=![]() =
=![]() ,
,
∴点E的坐标为(![]() ).
).
③当∠DBE=90°时,如图4.
此时PE=PA=6﹣t,OD=OC+BC﹣t=6﹣t.
则有OD=PE,EA=![]() =
=![]() (6﹣t)=6
(6﹣t)=6![]() ﹣
﹣![]() t,
t,
∴BE=BA﹣EA=4![]() ﹣(6
﹣(6![]() ﹣
﹣![]() t)=
t)=![]() t﹣2
t﹣2![]() .
.
∵PE∥OD,OD=PE,∠DOP=90°,∴四边形ODEP是矩形,
∴DE=OP=t,DE∥OP,∴∠BED=∠BAO=45°.
在Rt△DBE中,cos∠BED=![]() =
=![]() ,∴DE=
,∴DE=BE,
∴t=![]() t﹣2
t﹣2![]() )=2t﹣4.
)=2t﹣4.
解得:t=4,∴OP=4,PE=6﹣4=2,∴点E的坐标为(4,2).
综上所述:当以B、D、E为顶点的三角形是直角三角形时点E的坐标为(1,2)、(![]() )、(4,2).
)、(4,2).