��Ŀ����
����Ŀ�������һ��ƽ��ͼ�Σ������ֱ�ߺ�Բ�澭��������ͼ����Ƴ߹���ͼ��������һ����������ص������ȣ���ƵȻ�������ô�����ĵȻ�ת����Ϊ�صġ���������
��1���Ķ����
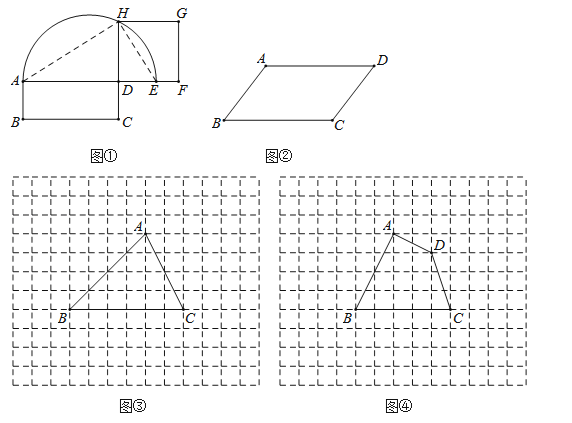
��ͼ�٣���֪����ABCD���ӳ�AD��E��ʹDE=DC����AEΪֱ������Բ���ӳ�CD����Բ�ڵ�H����DHΪ����������DFGH����������DFGH�����ABCD�Ȼ���
���ɣ�����AH��EH��
��AEΪֱ�������AHE=90�㣬���HAE+��HEA=90�㣮
��DH��AE�����ADH=��EDH=90��
���HAD+��AHD=90��
���AHD=��HED�����ADH�� ��
��![]() ����DH2=AD��DE��
����DH2=AD��DE��
�֡�DE=DC
��DH2= ����������DFGH�����ABCD�Ȼ���
��2������ʵ��
ƽ���ı��εġ�������˼·�ǣ��Ȱ�ƽ���ı���ת��Ϊ�Ȼ��ľ��Σ��ٰѾ���ת��Ϊ�Ȼ��������Σ�
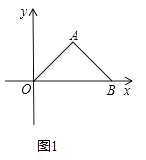
��ͼ�ڣ����ó߹���ͼ������ABCD�Ȼ��ľ��Σ���Ҫ��д����������������ͼ�ۼ�����
��3��������������εġ�������˼·�ǣ��Ȱ�������ת��Ϊ�Ȼ��� ����дͼ�����ƣ�����ת��Ϊ�Ȼ��������Σ�
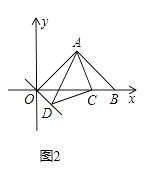
��ͼ�ۣ���ABC�Ķ���������������ĸ���ϣ����������ABC�Ȼ��������ε�һ���ߣ���Ҫ��д����������������ͼ�ۼ�����ͨ�������ABC�����ͼ����
��4����չ̽��
n���Σ�n��3���ġ�������˼·֮һ�ǣ���n����ת��Ϊ�Ȼ���n��1���Σ�����ֱ��ת��Ϊ�Ȼ��������Σ��Ӷ����Ի�����
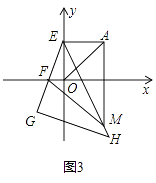
��ͼ�ܣ��ı���ABCD�Ķ���������������ĸ���ϣ����������ı���ABCD�Ȼ��������Σ���Ҫ��д����������������ͼ�ۼ�����ͨ�������ı���ABCD�����ͼ����
���𰸡���1����HDE��AD��DC����2����ͼ�������������3����������ͼ�������������4����ͼ�����������
��������
�����������1���������������ε��ж�������������ADH�ס�HDE�����ݵ����������ɵ�DH2=AD��DC��
��2���Ȱ�ƽ���ı���ABCDת��Ϊ�Ȼ��ľ���ADMN��Ȼ������������DFGH�����ABMN�Ȼ�������������DFGH��ƽ���ı���ABCD�Ȼ���
��3�����������εĵ�Ϊ���εij����������εĸߵ�һ��Ϊ���εĿ�������ABCת��Ϊ�Ȼ��ľ���MBCD��Ȼ���ӳ�MD��E��ʹDE=DC����MEΪֱ������Բ���ӳ�CD����Բ�ڵ�H����DH��Ϊ����ABC�Ȼ��������ε�һ���ߣ�
��4���ȸ�����AG��EH���õ�AG=2EH������CF=2DF���õ�CFEH=DFAG���ɴ˵ó�S��CEF=S��ADF��S��CDI=S��AEI������S��BCE=S�ı���ABCD������BCE���ı���ABCD�Ȼ���
�����������1����ͼ�٣�����AH��EH����AEΪֱ�������AHE=90�㣬���HAE+��HEA=90������DH��AE�����ADH=��EDH=90�㣬���HAD+��AHD=90�㣬���AHD=��HED�����ADH�ס�HDE����![]() ����DH2=AD��DE������DE=DC����DH2=AD��DC����������DFGH�����ABCD�Ȼ���
����DH2=AD��DE������DE=DC����DH2=AD��DC����������DFGH�����ABCD�Ȼ���
�ʴ�Ϊ����HDE��AD��DC��
��2����ͼ�ڣ��ӳ�AD��E��ʹDE=DM������AH��EH��������ADMN�ij��Ϳ��ֱ����ƽ���ı���ABCD�ĵߣ�������ADMN���������ƽ���ı���ABCD���������AEΪֱ�������AHE=90�㣬���HAE+��HEA=90������DH��AE�����ADH=��EDH=90�㣬���HAD+��AHD=90�㣬���AHD=��HED�����ADH�ס�HDE����![]() ����DH2=AD��DE������DE=DM����DH2=AD��DM����������DFGH�����ABMN�Ȼ�����������DFGH��ƽ���ı���ABCD�Ȼ���
����DH2=AD��DE������DE=DM����DH2=AD��DM����������DFGH�����ABMN�Ȼ�����������DFGH��ƽ���ı���ABCD�Ȼ���

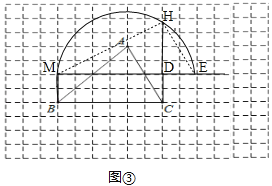
��3����ͼ�ۣ��ӳ�MD��E��ʹDE=DC������MH��EH��������MDBC�ij�������ABC�ĵף�����MDBC�Ŀ�������ABC�ĸߵ�һ�룬������MDBC�����������ABC���������MEΪֱ�������MHE=90�㣬���HME+��HEM=90������DH��ME�����MDH=��EDH=90�㣬���HMD+��MHD=90�㣬���MHD=��HED�����MDH�ס�HDE����![]() ����DH2=MD��DE������DE=DC����DH2=MD��DC����DH��Ϊ����ABC�Ȼ��������ε�һ������
����DH2=MD��DE������DE=DC����DH2=MD��DC����DH��Ϊ����ABC�Ȼ��������ε�һ������
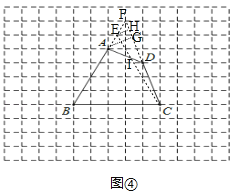
��4����ͼ�ܣ��ӳ�BA��CD���ڵ�F����AG��CF�ڵ�G��EH��CF�ڵ�H����BCE���ı���ABCD�Ȼ����������£���AG��EH����![]() ����AG=2EH������CF=2DF����CFEH=DFAG����S��CEF=S��ADF����S��CDI=S��AEI����S��BCE=S�ı���ABCD������BCE���ı���ABCD�Ȼ���
����AG=2EH������CF=2DF����CFEH=DFAG����S��CEF=S��ADF����S��CDI=S��AEI����S��BCE=S�ı���ABCD������BCE���ı���ABCD�Ȼ���

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�