Question

【题目】已知：如图所示，∠AOB：∠BOC=3：2，OD平分∠BOC，OE平分∠AOC，且∠DOE=36°，求∠BOE的度数．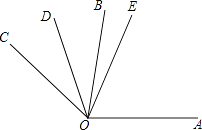

Answer 1

【答案】解：设∠AOB=3x，∠BOC=2x．
则∠AOC=∠AOB+∠BOC=5x．
∵OE是∠AOC的平分线，OD是∠BOC的平分线，
∴∠COE═ ∠AOC= x∠COD= ∠BOC=x，
∴∠DOE=∠COE﹣∠COD= x﹣x= x，
∵∠DOE=36°，
∴ x=36°，
解得，x=24°，
∴∠BOE=∠COE﹣∠COB= ×24﹣2×24=12°
【解析】根据已知∠AOB：∠BOC=3：2，设∠AOB=3x，∠BOC=2x，用含x的代数式表示出∠AOC，再根据角平分线的定义，用含x的代数式表示出∠COE，根据∠DOE=∠COE﹣∠COD，用含x的代数式表示出∠DOE，然后根据∠DOE=36°，求出x的值，即可得出结果。