题目内容
【题目】如图,在矩形ABCD中,E是边AD上一点(不与点A重合),连结BE,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连结BP、EQ.求证:四边形BPEQ是菱形.
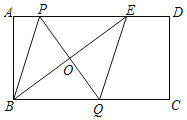
【答案】详见解析
【解析】
先根据线段垂直平分线的性质证明PB=PE,由ASA证明△BOQ≌△EOP,得出PE=QB,证出四边形BPEQ是平行四边形,再根据菱形的判定即可得出结论;
证明:∵PQ垂直平分BE,
∴PB=PE,OB=OE,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PEO=∠QBO,
在△BOQ与△EOP中,
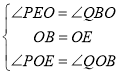 ,
,
∴△BOQ≌△EOP(ASA),
∴PE=QB,
又∵AD∥BC,
∴四边形BPEQ是平行四边形,
又∵QB=QE,
∴四边形BPEQ是菱形.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目