题目内容
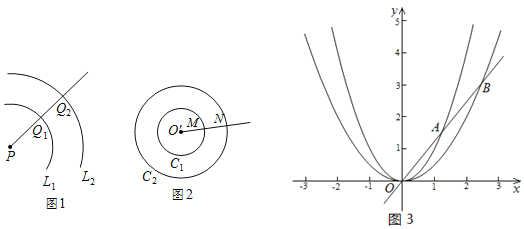
【题目】如图1,对于平面内的点P和两条曲线![]() 、
、![]() 给出如下定义:若从点P任意引出一条射线分别与
给出如下定义:若从点P任意引出一条射线分别与![]() 、
、![]() 交于
交于![]() 、
、![]() ,总有
,总有![]() 是定值,我们称曲线
是定值,我们称曲线![]() 与
与![]() “曲似”,定值
“曲似”,定值![]() 为“曲似比”,点P为“曲心”.
为“曲似比”,点P为“曲心”.
例如:如图2,以点![]() 为圆心,半径分别为
为圆心,半径分别为![]() 、
、![]() 都是常数
都是常数![]() 的两个同心圆
的两个同心圆![]() 、
、![]() ,从点
,从点![]() 任意引出一条射线分别与两圆交于点M、N,因为总有
任意引出一条射线分别与两圆交于点M、N,因为总有![]() 是定值,所以同心圆
是定值,所以同心圆![]() 与
与![]() 曲似,曲似比为
曲似,曲似比为![]() ,“曲心”为
,“曲心”为![]() .
.
![]() 在平面直角坐标系xOy中,直线
在平面直角坐标系xOy中,直线![]() 与抛物线
与抛物线![]() 、
、![]() 分别交于点A、B,如图3所示,试判断两抛物线是否曲似,并说明理由;
分别交于点A、B,如图3所示,试判断两抛物线是否曲似,并说明理由;
![]() 在
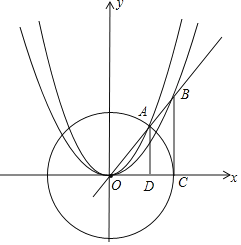
在![]() 的条件下,以O为圆心,OA为半径作圆,过点B作x轴的垂线,垂足为C,是否存在k值,使
的条件下,以O为圆心,OA为半径作圆,过点B作x轴的垂线,垂足为C,是否存在k值,使![]() 与直线BC相切?若存在,求出k的值;若不存在,说明理由;
与直线BC相切?若存在,求出k的值;若不存在,说明理由;
![]() 在
在![]() 、
、![]() 的条件下,若将“
的条件下,若将“![]() ”改为“
”改为“![]() ”,其他条件不变,当存在
”,其他条件不变,当存在![]() 与直线BC相切时,直接写出m的取值范围及k与m之间的关系式.
与直线BC相切时,直接写出m的取值范围及k与m之间的关系式.
【答案】(1)两抛物线曲似,理由详见解析;(2)存在k值,使![]() 与直线BC相切,
与直线BC相切,![]() ;(3)
;(3)![]() ,
,![]() .
.
【解析】
![]() 过点A、B作x轴的垂线,垂足分别为D、C,根据题意可得
过点A、B作x轴的垂线,垂足分别为D、C,根据题意可得![]() 、
、![]() 、
、![]() 、
、![]() ,由
,由![]() 知
知![]() ,据此可可解答;
,据此可可解答;![]() 假设存在k值,使
假设存在k值,使![]() 与直线BC相切,据此知
与直线BC相切,据此知![]() ,根据
,根据![]() 及对称性可得答案;
及对称性可得答案;![]() 同理可得
同理可得![]() 、
、![]() 、
、![]() 、
、![]() ,由切线性质知
,由切线性质知![]() ,根据
,根据![]() 可得m的范围,由
可得m的范围,由![]() 可得k与m之间的关系式.
可得k与m之间的关系式.
![]() 是,
是,
过点A、B作x轴的垂线,垂足分别为D、C,
依题意可得![]() 、
、![]() ,
,
因此![]() 、
、![]() ,
,
![]() 轴、
轴、![]() 轴,
轴,
![]() ,
,
![]() ,
,
![]() 两抛物线曲似,曲似比为
两抛物线曲似,曲似比为![]() ;
;
![]() 假设存在k值,使
假设存在k值,使![]() 与直线BC相切,
与直线BC相切,
则![]() ,
,
又![]() 、
、![]() ,并且
,并且![]() ,
,
![]() ,
,
解得:![]() 负值舍去
负值舍去![]() ,
,
由对称性可取![]() ,
,
综上,![]() ;
;
![]() 根据题意得
根据题意得![]() 、
、![]() ,
,
因此![]() 、
、![]() ,
,
![]() 与直线BC相切,
与直线BC相切,
![]() ,
,
由![]() 可得
可得![]() ,
,
则![]() ,
,
由![]() 、
、![]() ,并且
,并且![]() ,
,
![]() ,
,
整理,得:![]() .
.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目