题目内容
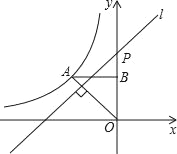
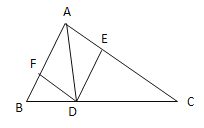
【题目】如图,在等边△ABC中,点E在线段AC上,连接BE,点D在直线BC上,且CE=CD,连接ED、AD,点F是BE的中点,连接FA、FD.
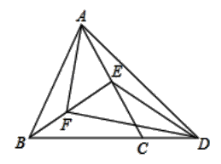
(1)若CD=6,BC=10,求△BEC的面积;
(2)当AE=CE时,求证:AD=2AF.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)作EH⊥BC于H.在直角三角形ECH中求出EH,即可解决问题.
(2)如图1过点B作BG∥AC交AF的延长线于G,先证明△BFG≌△EFA,再证明△ABG≌△ACD,即可解决问题.
(1)如图,作EH⊥BC于H.
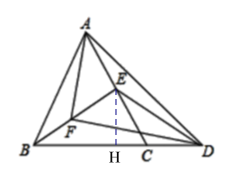
∴∠EHC=90°
∵△ABC是等边三角形
∴∠ECH=60°
∴∠HEC=30°
∵CE=CD=6,
∴![]() ,
,![]()
∴S△BEC=![]() BCEH=
BCEH=![]()
(2)如图,过点B作BG∥AC交AF的延长线于G,

∴∠G=∠EAF,∠CBG=∠ACB=60°
∴∠ABG=∠ABC+∠CBG=120°=∠ACD
∵点F是BE中点
∴BF=EF
在△BFG和△EFA中
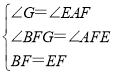
∴△BFG≌△EFA
∴BG=AE,AF=FG
∵AE=EC=CD
∴BG=CD
在△ABG和△ACD中,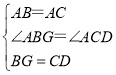
∴△ABG≌△ACD,
∴AD=AG=2AF.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目