题目内容
【题目】如图,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
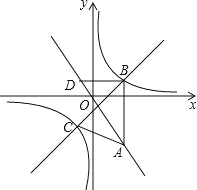
,![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,且
,且 ![]() ,
,![]() 满足
满足![]() .
.
(1)写出![]() 、
、![]() 两点坐标;
两点坐标;
(2)求![]() 点坐标;
点坐标;
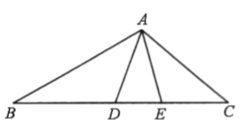
(3)如图,![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() ,请写出线段
,请写出线段![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
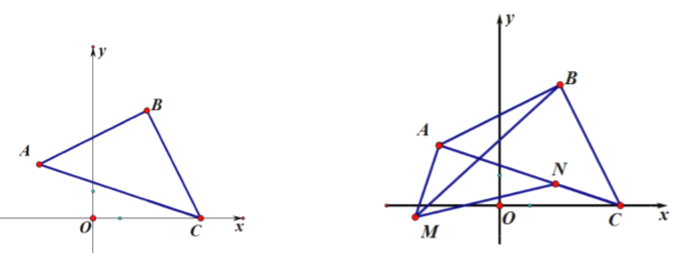
【答案】(1)点A的坐标为![]() ,点C的坐标为
,点C的坐标为![]() ;(2)点B的坐标为(2,4);(3)MN= CN+AM,理由见解析
;(2)点B的坐标为(2,4);(3)MN= CN+AM,理由见解析
【解析】
(1)根据绝对值的非负性和平方的非负性即可求出a、b的值,从而求出![]() 、
、![]() 两点坐标;
两点坐标;
(2)过点A作AE∥y轴,过点B作BE⊥AE,作BD⊥x轴,设点B的坐标为(x,y),分别用x、y表示出CD、BE、AE的长,然后利用AAS证出△EBA≌△DBC,可得BE=BD,AE=CD,列出方程即可求出点B的坐标;
(3)过点B作BF⊥BM,交AC的延长线与点F,连接MF,利用SAS证出△ABM≌△CBF,从而得到AM=CF,BM=BF,∠AMB=∠CFB,根据等边对等角可得∠BMF=∠BFM,然后证出∠FMN=∠MFN,再根据等角对等边可得MN=NF,即可得出结论.
解:(1)∵![]()
∴![]()
∵![]()
∴![]()
解得:a=-2,b=2
∴点A的坐标为![]() ,点C的坐标为
,点C的坐标为![]() ;
;
(2)过点A作AE∥y轴,过点B作BE⊥AE,作BD⊥x轴,如下图所示
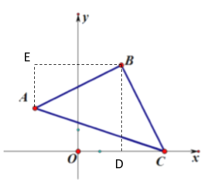
设点B的坐标为(x,y)
∴BD=y,OD=x
∴CD=4-x,BE=x-(-2)=x+2,AE=y-2
∵BD⊥x轴
∴BD∥y轴
∴AE∥BD
∴∠DBE=180°-∠AEB=90°
∴∠EBA+∠ABD=90°
∵等腰直角三角形![]() 中,
中,![]() ,
,![]()
∴∠DBC+∠ABD=90°
∴∠EBA=∠DBC
在△EBA和△DBC中
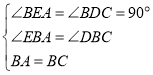
∴△EBA≌△DBC
∴BE=BD,AE=CD
即x+2= y,y-2=4-x
解得:x=2,y=4
∴点B的坐标为(2,4);
(3)MN= CN+AM,理由如下
过点B作BF⊥BM,交AC的延长线与点F,连接MF
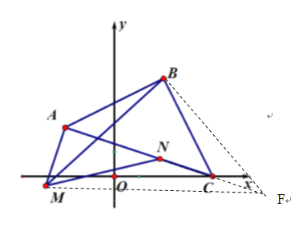
∴∠MBC+∠CBF=90°
∵△ABC为等腰三角形
∴BA=BC,∠BAC=∠BCA=45°,∠ABC=90°
∴∠MBC+∠ABM=90°,∠BCF=180°-∠BCA=135°,∠BAM=∠MAC+∠BAC=135°
∴∠ABM =∠CBF,∠BAM=∠BCF
在△ABM和△CBF中
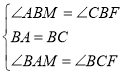
∴△ABM≌△CBF
∴AM=CF,BM=BF,∠AMB=∠CFB
∴∠BMF=∠BFM,
∵![]()
∴∠NMB=∠CFB
∴∠BMF-∠NMB=∠BFM-∠CFB
∴∠FMN=∠MFN
∴MN=NF
∵NF=CN+CF
∴MN=CN+AM

 名校课堂系列答案
名校课堂系列答案