题目内容
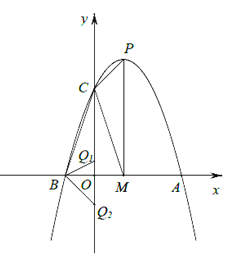
【题目】平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx+3与y轴相交于点C,与x轴正半轴相交于点A,OA=OC,与x轴的另一个交点为B,对称轴是直线x=1,顶点为P.
(1)求这条抛物线的表达式和顶点P的坐标;
(2)抛物线的对称轴与x轴相交于点M,求∠PMC的正切值;
(3)点Q在y轴上,且△BCQ与△CMP相似,求点Q的坐标.

【答案】(1)(1,4)(2)(0, ![]() )或(0,-1)
)或(0,-1)
【解析】试题分析:(1)先求得点C的坐标,再由OA=OC得到点A的坐标,再根据抛物线的对称性得到点B的坐标,利用待定系数法求得解析式后再进行配方即可得到顶点坐标;
(2)由OC//PM,可得∠PMC=∠MCO,求tan∠MCO即可 ;
(3)分情况进行讨论即可得.
试题解析:(1)当x=0时,抛物线y=ax2+bx+3=3,所以点C坐标为(0,3),∴OC=3,
∵OA=OC,∴OA=3,∴A(3,0),
∵A、B关于x=1对称,∴B(-1,0),
∵A、B在抛物线y=ax2+bx+3上,
∴![]() ,∴
,∴![]() ,
,
∴抛物线解析式为:y=-x2+2x+3=-(x-1)2+4,
∴顶点P(1,4);
(2)由(1)可知P(1,4),C(0,3),所以M(1,0),∴OC=3,OM=1,
∵OC//PM,∴∠PMC=∠MCO,
∴tan∠PMC=tan∠MCO=![]() =
=![]() ;
;
(3)Q在C点的下方,∠BCQ=∠CMP,
CM=![]() ,PM=4,BC=
,PM=4,BC=![]() ,
,
∴![]() 或
或![]() ,
,
∴CQ=![]() 或4,
或4,
∴Q1(0, ![]() ),Q2(0,-1).
),Q2(0,-1).

练习册系列答案
相关题目