Question

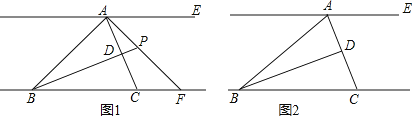
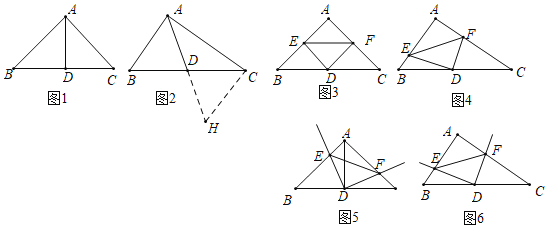
【题目】如图1，Rt△ABC中，∠A＝90°，AB＝AC，点D是BC边的中点连接AD，则易证AD＝BD＝CD，即AD＝BC；如图2，若将题中AB＝AC这个条件删去，此时AD仍然等于BC．

理由如下：延长AD到H，使得AH＝2AD，连接CH，先证得△ABD≌△CHD，此时若能证得△ABC≌△CHA，

即可证得AH＝BC，此时AD＝BC，由此可见倍长过中点的线段是我们三角形证明中常用的方法．

（1）请你先证明△ABC≌△CHA，并用一句话总结题中的结论；

（2）现将图1中△ABC折叠（如图3），点A与点D重合，折痕为EF，此时不难看出△BDE和△CDF都是等腰直角三角形．BE＝DE，CF＝DF．由勾股定理可知DE2+DF2＝EF2，因此BE2+CF2＝EF2，若图2中△ABC也进行这样的折叠（如图4），此时线段BE、CF、EF还有这样的关系式吗？若有，请证明；若没有，请举反例．

（3）在（2）的条件下，将图3中的△DEF绕着点D旋转（如图5），射线DE、DF分别交AB、AC于点E、F，此时（2）中结论还成立吗？请说明理由．图4中的△DEF也这样旋转（如图6），直接写出上面的关系式是否成立．

Answer 1

【答案】（1）详见解析；（2）有这样分关系式；（3）EF2＝BE2+CF2.

【解析】

（1）想办法证明AB∥CH，推出∠BAC＝∠ACH，再利用SAS证明△ABC≌△CHA即可．

（2）有这样分关系式．如图4中，延长ED到H山顶DH＝DE．证明△EDB≌△HD（SAS），推出∠B＝∠HCD，BE＝CH，∠FCH＝90°，利用勾股定理，线段的垂直平分线的性质即可解决问题．

（3）图5，图6中，上面的关系式仍然成立．

（1）证明：如图2中，

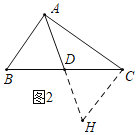
∵BD＝DC，∠ADB＝∠HDC，AD＝HD，

∴△ADB≌△HDC（SAS），

∴∠B＝∠HCD，AB＝CH，

∴AB∥CH，

∴∠BAC+∠ACH＝180°，

∵∠BAC＝90°，

∴∠ACH＝∠BAC＝90°，

∵AC＝CA，

∴△BAC≌△HCA（SAS），

∴AH＝BC，

∴AD＝DH＝BD＝DC，

∴AD＝BC．

结论：直角三角形斜边上的中线等于斜边的一半．

（2）解：有这样分关系式．

理由：如图4中，延长ED到H山顶DH＝DE．

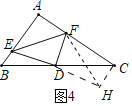
∵ED＝DH，∠EDB＝∠HDC，DB＝DC，

∴△EDB≌△HDC（SAS），

∴∠B＝∠HCD，BE＝CH，

∵∠B+∠ACB＝90°，

∴∠ACB+∠HCD＝90°，

∴∠FCH＝90°，

∴FH2＝CF2+CH2，

∵DF⊥EH，ED＝DH，

∴EF＝FH，

∴EF2＝BE2+CF2．

（3）图5，图6中，上面的关系式仍然成立．结论：EF2＝BE2+CF2．

证明方法类似（2）．