题目内容
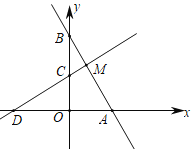
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+2
x+2![]() 交x轴于点A,交y轴于点B.
交x轴于点A,交y轴于点B.
(1)求∠OAB的度数;
(2)点M是直线y=﹣![]() x+2
x+2![]() 上的一个动点,且⊙M的半径为2,圆心为M,判断原点O与⊙M的位置关系,并说明理由;
上的一个动点,且⊙M的半径为2,圆心为M,判断原点O与⊙M的位置关系,并说明理由;
(3)当⊙M与y轴相切时,直接写出切点的坐标.

【答案】(1)30°;(2)点O在圆M外,理由见解析;(3)(0,![]() )或(0,
)或(0,![]() )
)
【解析】
(1)分别求出A与B的坐标,求出OA与OB的长,利用直角三角形性质判断即可;
(2)求出点O与圆心M的距离,与半径比较大小即可;
(3)分M在第一象限与第二象限两种情况,利用切线的性质及直角三角形的性质确定出切点坐标即可.
解:(1)直线y=﹣![]() x+2
x+2![]() ,
,
令x=0,得到y=2![]() ;令y=0,得到x=6,
;令y=0,得到x=6,
∴OA=6,OB=2![]() ,
,
在Rt△AOB中,tan∠OAB=![]() =
=![]() ,
,
则∠OAB=30°;
(2)点O在圆M外,理由为:
当OM⊥AB时,点M距离点O最近,此时OM=3,
∵3>2,
∴点O在圆M外;
(3)当点M在第一象限时,设此时圆M与y轴相切于点N,可得MN=2,
∵∠BMN=∠BAO=30°,
∴设BN=x,则有BM=2x,
根据勾股定理得:x2+22=(2x)2,
解得:x=![]() ,即ON=OB﹣BN=2
,即ON=OB﹣BN=2![]() ﹣
﹣![]() =
=![]() ,
,
此时N坐标为(0,![]() );
);
当点M在第二象限时,设此时圆M′与y轴相切于点N′,同理可得BN=′![]() ,
,
此时ON′=OB+BN′=![]() ,N坐标为(0,
,N坐标为(0,![]() ),
),
综上,圆M与y轴相切时,切点坐标为(0,![]() )或(0,
)或(0,![]() ).
).

练习册系列答案
相关题目