题目内容
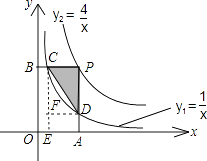
【题目】如图,已知双曲线 ![]() ,
, ![]() ,点P为双曲线
,点P为双曲线 ![]() 上的一点,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别依次交双曲线
上的一点,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别依次交双曲线 ![]() 于D、C两点,则△PCD的面积为 .
于D、C两点,则△PCD的面积为 . 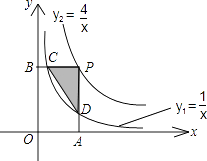
【答案】![]()
【解析】解:作CE⊥AO于E,DF⊥CE于F, ∵双曲线 ![]() ,
, ![]() ,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别依次交双曲线
,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别依次交双曲线 ![]() 于D、C两点,
于D、C两点,
∴矩形BCEO的面积为:xy=1,
∵BC×BO=1,BP×BO=4,
∴BC= ![]() BP,
BP,
∵AO×AD=1,AO×AP=4,
∴AD= ![]() AP,
AP,
∵PAPB=4,
∴ ![]() PB×
PB× ![]() PA=
PA= ![]() PAPB=CP×DP=
PAPB=CP×DP= ![]() ×4=
×4= ![]() ,
,
∴△PCD的面积为: ![]() .
.
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解比例系数k的几何意义的相关知识,掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.

【题目】某校为了解七年级男生体操测试情况,随机抽取了50名男生的测试成绩进行统计,根据评分标准,将他们的成绩分为A,B,C,D四个等级,并绘制成频数分布表和扇形统计图(如图).
等级 | 成绩x/分 | 频数/(人数) | 频率 |
A | 9.0≤x≤10.0 | a | m |
B | 7.0≤x<9.0 | 23 | 0.46 |
C | 6.0≤x<7.0 | b | n |
D | 0.0≤x<6.0 | 3 | 0.06 |
合计 | 50 | 1.00 |
(1)在被调查的男生中,成绩为B等级的有多少人,占被调查男生人数的多少,m 等于 多少;
(2)求a,b,n的值;
(3)如果该校七年级共有200名男生,试估计这200名男生中成绩达到A等级和B等级的共有多少人.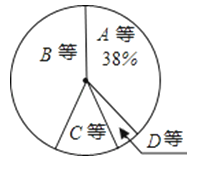
【题目】将自然数按如表规律排列,表中数2在第二行第一列,与有序数对![]() 对应,数5与
对应,数5与![]() 对应,数14与
对应,数14与![]() 对应,根据这一规律,数2014对应的有序数对为__________.
对应,根据这一规律,数2014对应的有序数对为__________.
第一列 | 第二列 | 第三列 | 第四列 | 第五列 | ||
第一行 | 1 | 4 | 5 | 16 | 17 | … |
第二行 | 2 | 3 | 6 | 15 | … | |
第三行 | 9 | 8 | 7 | 14 | … | |
第四行 | 10 | 11 | 12 | 13 | … | |
第五行 | … | |||||
…… |