题目内容
【题目】如图，等腰梯形ABCD中，AD∥BC，∠B=45°，P是BC边上一点，△PAD的面积为 
，设AB=x，AD=y
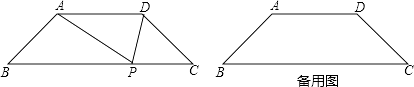
（1）求y与x的函数关系式；
（2）若∠APD=45°，当y=1时，求PBPC的值；
（3）若∠APD=90°，求y的最小值．
【答案】
（1）
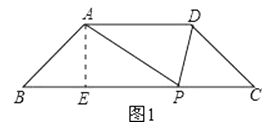
解：如图1，过A作AE⊥BC于点E，
在Rt△ABE中，∠B=45°，AB=x，
∴AE=ABsinB= 
x，
∵S△APD= 
ADAE= ，
∴ y x= ，
则y= 
（2）
解：∵∠APC=∠APD+∠CPD=∠B+∠BAP，∠APD=∠B=45°，
∴∠BAP=∠CPD，
∵四边形ABCD为等腰梯形，
∴∠B=∠C，
∴△ABP∽△PCD，
∴ 
= 
，
∴PBPC=ABDC=AB2，
当y=1时，x= 
，即AB= ，
则PBPC=（ ）2=2
（3）
解：如图2，取AD的中点F，连接PF，
过P作PH⊥AD，可得PF≥PH，
当PF=PH时，PF有最小值，
又∵∠APD=90°，
∴PF= AD= y，
∴PH= y，
∵S△APD= ADPH= ，
∴ y y≥ ，即y2≥2，
∵y＞0，
∴当取“=“时，y取最小值 ，
则y的最小值为
【解析】（1）如图1，过A作AE垂直于BC，在直角三角形ABE中，由∠B=45°，AB=x，利用锐角三角函数定义表示出AE，三角形PAD的面积以AD为底，AE为高，利用三角形面积公式表示出，根据已知的面积即可列出y与x的函数关系式；（2）根据∠APC=∠APD+∠CPD，以及∠APC为三角形ABP的外角，利用外角性质得到关系式，等量代换得到∠BAP=∠CPD，再由四边形ABCD为等腰梯形，得到一对底角相等及AB=CD，可得出三角形ABP与三角形PDC相似，由相似得比例，将CD换为AB，由y的值求出x的值，即为AB的值，即可求出PBPC的值；（3）取AD的中点F，过P作PH垂直于AD，由直角三角形PF大于等于PH，当PF=PH时，PF最小，此时F与H重合，由三角形APD为直角三角形，利用直角三角形斜边上的中线等于斜边的一半得到PF等于AD的一半，表示出PF即为PH，三角形APD面积以AD为底，PH为高，利用三角形面积公式表示出三角形APD面积，由已知的面积求出y的值，即为最小值．
【考点精析】解答此题的关键在于理解三角形的外角的相关知识，掌握三角形一边与另一边的延长线组成的角，叫三角形的外角；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角，以及对等腰梯形的性质的理解，了解等腰梯形的两腰相等；同一底上的两个角相等；两条对角线相等．
