Question

【题目】已知二次函数y=-3x+．

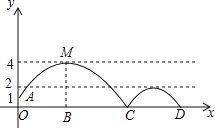
（1）该二次函数图象与x轴的交点坐标是______；

（2）将y=化成y=a（x-h）2+k的形式，并写出顶点坐标；

（3）在坐标轴中画出此抛物线的大致图象；

（4）写出不等式＞0的解集．

Answer 1

【答案】（1）（1，0），（5，0）；（2）y=（x-3）2-2，（3，2）；（3）见解析；（4）x＜1或x＞5．

【解析】

（1）解方程x2-3x+=0，解得该二次函数图象与x轴的交点坐标；

（2）利用配方法得到y=（x-3）2-2，从而得到抛物线的顶点坐标；

（3）利用描点法画出二次函数的图象；

（4）利用函数图象，写出抛物线在x轴上方所对应的自变量的范围即可．

（1）当y=0时，-3x+=0，解得x1=1，x2=5，

所以该二次函数图象与x轴的交点坐标为（1，0），（5，0）；

故答案为：（1，0），（5，0）；

（2）y=-3x+=（x2-6x）+=（x2-6x+9-9）+=（x-3）2-2，

所以二次函数图象的顶点坐标为（3，2）；

（3）当x=0时，y=x2-3x+=，则抛物线与y轴的交点坐标为（0，），

如图，

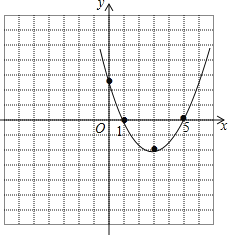
（4）不等式x2-3x+＞0的解集为x＜1或x＞5.