题目内容
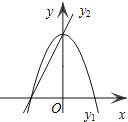
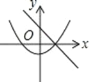
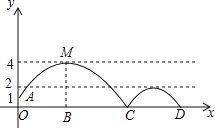
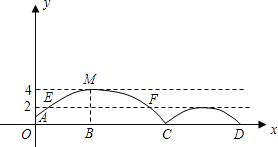
【题目】如图,足球场上守门员在O处踢出一高球,球从离地面1m的A处飞出(A在y轴上),运动员乙在距O点6m的B处发现球在自己头的正上方达到最高点M,距地面有4m高,球落地后又一次弹起,第二个落点为D,据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的解析式;
(2)求足球第一次落地点C处距守门员有多少米?(取![]() ≈1.7)
≈1.7)
(3)运动员乙要抢到第二个落点D处的球,他应再向前跑多少米?(取![]() ≈2.5)
≈2.5)
【答案】(1)y=-![]() (x-6)2+4;(2)13米;(3)17米.
(x-6)2+4;(2)13米;(3)17米.
【解析】
(1)由条件可以得出M(6,4),设抛物线的解析式为y=a(x-6)2+4,由待定系数法求出其解即可;
(2)当y=0时代入(1)的解析式,求出x的值即可;
(3)设第二次抛物线的顶点坐标为(m,2),抛物线的解析为y=a(x-m)2+2,求出解析式,就可以求出OD的值,进而得出结论.
解:(1)根据题意,可设第一次落地时,抛物线的表达式为y=a(x-6)2+4,
将点A(0,1)代入,得:36a+4=1,
解得:a=-![]() ,
,
∴足球开始飞出到第一次落地时,该抛物线的表达式为y=-![]() (x-6)2+4;
(x-6)2+4;
(2)令y=0,得:-![]() (x-6)2+4=0,
(x-6)2+4=0,
解得:x1=4![]() +6≈13,x2=-4
+6≈13,x2=-4![]() +6<0(舍去),
+6<0(舍去),
∴足球第一次落地点C距守门员13米;
(3)如图,足球第二次弹出后的距离为CD,
根据题意知CD=EF(即相当于将抛物线AEMFC向下平移了2个单位),
∴-![]() (x-6)2+4=2,
(x-6)2+4=2,
解得:x1=6-2![]() ,x2=6+2
,x2=6+2![]() ,
,
∴CD=x2-x1=4![]() ≈10,
≈10,
∴BD=13-6+10=17米,
答:运动员乙要抢到足球第二个落点D,他应再向前跑17米.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目