题目内容
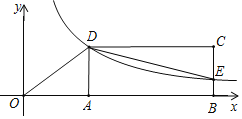
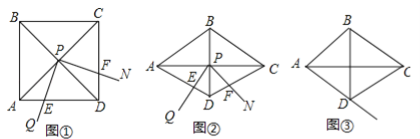
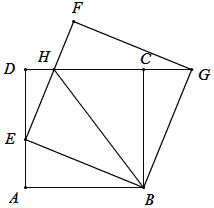
【题目】如图,正方形ABCD的边长为2,点E是AD边上的动点,从点A开始沿AD向D运动.以BE为边,在BE的上方作正方形BEFG,EF交DC于点H,连接CG、BH.请探究:
(1)线段AE与CG是否相等?请说明理由.
(2)若设AE=x,DH=y,当x取何值时,y最大?最大值是多少?
(3)当点E运动到AD的何位置时,△BEH∽△BAE?
【答案】(1)AE=CG,见解析;(2)当x=1时,y有最大值,为![]() ;(3)当E点是AD的中点时,△BEH∽△BAE,见解析.
;(3)当E点是AD的中点时,△BEH∽△BAE,见解析.
【解析】
(1)由正方形的性质可得AB=BC,BE=BG,∠ABC=∠EBG=90°,由“SAS”可证△ABE≌△CBG,可得AE=CG;
(2)由正方形的性质可得∠A=∠D=∠FEB=90°,由余角的性质可得∠ABE=∠DEH,可得△ABE∽△DEH,可得![]() ,由二次函数的性质可求最大值;
,由二次函数的性质可求最大值;
(3)当E点是AD的中点时,可得AE=1,DH=![]() ,可得
,可得![]() ,且∠A=∠FEB=90°,即可证△BEH∽△BAE.
,且∠A=∠FEB=90°,即可证△BEH∽△BAE.
(1)AE=CG,理由如下:
∵四边形ABCD,四边形BEFG是正方形,
∴AB=BC,BE=BG,∠ABC=∠EBG=90°,
∴∠ABE=∠CBG,且AB=BC,BE=BG,
∴△ABE≌△CBG(SAS),
∴AE=CG;
(2)∵四边形ABCD,四边形BEFG是正方形,
∴∠A=∠D=∠FEB=90°,
∴∠AEB+∠ABE=90°,∠AEB+∠DEH=90°,
∴∠ABE=∠DEH,
又∵∠A=∠D,
∴△ABE∽△DEH,
∴![]() ,
,
∴![]()
∴![]() =
=![]() ,
,
∴当x=1时,y有最大值为![]() ;
;
(3)当E点是AD的中点时,△BEH∽△BAE,
理由如下:
∵E是AD中点,
∴AE=1,
∴![]()
又∵△ABE∽△DEH,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,且∠DAB=∠FEB=90°,
,且∠DAB=∠FEB=90°,
∴△BEH∽△BAE.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案