Question

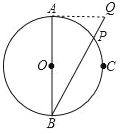
【题目】如图，AB为⊙O的直径，AB=4，C为半圆AB的中点，P为上一动点，延长BP至点Q，使BPBQ=AB2．若点P由A运动到C，则点Q运动的路径长为_____．

Answer 1

【答案】4

【解析】

连接AQ，由BPBQ=AB2，可证,从而可证△ABP∽△QBA，由相似三角形的性质知∠APB=∠QAB=90°，即QA始终与AB垂直.根据三角形中位线定理即可求出Q运动的路径长.

如图所示：连接AQ．

∵BPBQ=AB2，

∴=．

又∵∠ABP=∠QBA，

∴△ABP∽△QBA，

∴∠APB=∠QAB=90°，

∴QA始终与AB垂直．

当点P在A点时，Q与A重合，

当点P在C点时，OC是中位线，则AQ=2OC=4，此时，Q运动到最远处，

∴点Q运动路径长为4．

故答案为：4．