题目内容
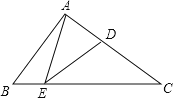
【题目】如图,在Rt△ABC中,已知∠BAC=90°,AB=6,AC=8,点D是AC上的一点,将△ABC沿着过点D的一条直线翻折,使点C落在BC边上的点E处,连接AE、DE,当∠CDE=∠AEB时,AE的长是______.
【答案】![]()
【解析】
分别过A、D点作AM、DN垂直于BC与M、N点,利用三角形内角和180°,以及平角180度,推导出ED平分∠AEC,则DA=DN,设DN=DA=x,则CD=8-x,利用三角函数求出ED、DN长,从而确定了EN和CN长为4,可求BE=2,利用三角函数知识求出AM、BM值,最后在Rt△AEM中利用勾股定理求的AE长.
由勾股定理可得BC=10.
分别过A、D点作AM、DN垂直于BC与M、N点,
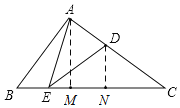
根据折叠的性质可知∠C=∠DEC,EN=CN,
∵∠DEC+∠C+∠EDC=180°,∠DEC+∠AED+∠AEB=180°,
已知∠EDC=∠AEB,∴∠AED=∠DCE=∠DEC,即ED平分∠AEC,
根据角平分线的性质可得DN=DA,
设DN=DA=x,则CD=8-x,
sinC=![]() ,即
,即![]() ,
,
解得x=3,
所以DN=3,CD=5,
所以NC=4,EN=4,
所以BE=10-4-4=2,
sinB=![]() ,即
,即![]() ,解得AM=4.8,
,解得AM=4.8,
在Rt△ABM中利用勾股定理可得BM=3.6,
则EM=3.6-2=1.6,
在Rt△AEM中,AE=![]() .
.

练习册系列答案
相关题目