题目内容
【题目】甲、乙两辆汽车沿同一路线赶赴距出发地480km的目的地，乙车比甲车晚出发2h（从甲车出发时开始计时）．图中折线OABC、线段DE分别表示甲、乙两车所行路程y（km）与时间x（h）之间的函数关系对应的图象（线段AB表示甲车出发不足2h因故障停车检修）．请根据图象所提供的信息，解决以下问题：
（1）求乙车所行路程y与时间x之间的函数关系式；
（2）求两车在途中第二次相遇时，它们距出发地的路程；
（3）乙车出发多长时间，两车在途中第一次相遇．（写出解题过程）
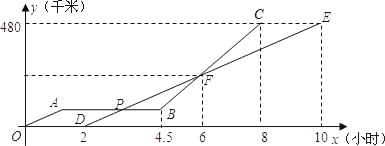
【答案】（1）y与x的函数关系式为y=60x﹣120；（2）两车在途中第二次相遇时，它们距出发地的路程为240千米；（3）乙车出发3﹣2=1小时，两车在途中第一次相遇
【解析】分析：（1）由图可看出，乙车所行路程y与时间x的成一次函数，使用待定系数法可求得一次函数关系式；
（2）由图可得，交点F表示第二次相遇，F点横坐标为6，代入（1）中的函数即可求得距出发地的路程；
（3）交点P表示第一次相遇，即甲车故障停车检修时相遇，点P的横坐标表示时间，纵坐标表示离出发地的距离，要求时间，则需要把点P的纵坐标先求出；从图中看出，点P的纵坐标与点B的纵坐标相等，而点B在线段BC上，BC对应的函数关系可通过待定系数法求解，点B的横坐标已知，则纵坐标可求．
详解：（1）设乙车所行路程y与时间x的函数关系式为y=k1x+b1，
把（2，0）和（10，480）代入，
得
，解得
，
∴y与x的函数关系式为y=60x-120；
（2）由图可得，交点F表示第二次相遇，
而F点横坐标为6，此时y=60×6-120=240，
∴F点坐标为（6，240），
∴两车在途中第二次相遇时，它们距出发地的路程为240千米；
（3）设线段BC对应的函数关系式为y=k2x+b2，
把（6，240）、（8，480）代入，
得
，
解得
，
∴y与x的函数关系式为y=120x-480，
∴当x=4.5时，y=120×4.5-480=60．
∴点B的纵坐标为60，
∵AB表示因故停车检修，
∴交点P的纵坐标为60，
把y=60代入y=60x-120中，
有60=60x-120，
解得x=3，
∴交点P的坐标为（3，60），
∵交点P表示第一次相遇，
∴乙车出发3-2=1小时，两车在途中第一次相遇．
