题目内容
【题目】如图,已知点A在数轴上对应的数为x,点B对应的数为y,且点O为数轴上的原点,且![]() .
.
![]()
(1)点A对应的数为______;点B对应的数为______;线段![]() 的长度为_______;
的长度为_______;
(2)若数轴上有一点C,且![]() ,求点C在数轴上对应的数;
,求点C在数轴上对应的数;
(3)若点P从A点出发沿数轴的正方向以每秒2个单位的速度运动,同时Q点从B点出发沿数轴的负方向以每秒4个单位长度的速度运动,运动时间为t秒,当![]() 时,求t的值.
时,求t的值.
【答案】(1)-5;4;9;(2)-8或7;(3)![]() 和
和![]() .
.
【解析】
(1)由绝对值和偶次方的非负性即可求出a、b值;
(2)根据AB=9可知点C在点A的左侧或点B的右侧,分点C在点A左侧和点C在点B右侧两种情况考虑,找出AC、BC的长度结合AC+BC=15即可得出关于x的一元一次方程,解之即可得出结论;
(3)根据点P、Q的运动找出OP、OQ的长度,结合OP=2OQ即可得出关于t的含绝对值符号的一元一次方程,解之即可得出结论.
(1)∵|a+5|+(a+b+1)2=0,
∴a+5=0,a+b+1=0,
∴a=-5,b=4.
∴AB=|4-(-5)|=9,
(2)设点C在数轴上对应的数为x,
∵AB=4-(-5)=9,
∴点C在点A的左侧或点B的右侧,
若点C在点A左侧,则AC=-5-x,BC=4-x,如图1所示.
![]()
∴AC+BC=-5-x+4-x=-1-2x=15,
解得:x=-8;
若点C在点B右侧,则AC=x-(-5)=x+5,BC=x-4,
∴AC+BC=x+5+x-4=15,
解得:x=7.
∴点C在数轴上对应的数为-8或7.
(3)OP=|5-2t|,OQ=|4-4t|,如图2所示.
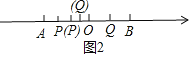
∵OP=2OQ,
∴|5-2t|=2|4-4t|,
解得:t1=![]() ,t2=
,t2=![]() .
.
∴当OP=2OQ时,t的值为![]() 和
和![]() .
.

【题目】移动公司推出一款话费套餐活动,资费标准见下表
套餐月费/元 | 套餐内容 | 套餐外资费 | |
主叫限定时间/分钟 | 被叫 | 主叫超时费(元/分钟) | |
58 | 50 | 免费 | 0.25 |
88 | 150 | 0.20 | |
118 | 350 | 0.15 | |
说明:①主叫:主动打电话给别人;被叫:接听别人打进来的电话. ②若办理的是月使用费为58元的套餐,主叫时间不超过50分钟时,当月话费即为58元;主叫时间为60分钟,则当月话费为 | |||
小文办理的是月使用费为88元的套餐,亮亮办理的是月使用费为118元的套餐.
(1)①小文当月的主叫时间为220分钟,则该月她的话费为__________元.
②亮亮当月的主叫时间为220分钟,则该月他的话费为____________元.
(2)某月小文与亮亮的主叫时间都为m分钟(![]() ),请用含m的代数式表示该月他们的话费差.
),请用含m的代数式表示该月他们的话费差.
(3)11月小文和亮亮的话费相同,但主叫时间比亮亮少100分钟,则小文的主叫时间是_______分钟.