Question

【题目】如图，A，B，C，D为四家超市，其中超市D距A，B，C三家超市的路程分别为25km，10km，5km．现计划在A，D之间的道路上建一个配货中心P，为避免交通拥堵，配货中心与超市之间的距离不少于2km．假设一辆货车每天从P出发为这四家超市送货各1次，由于货车每次仅能给一家超市送货，因此每次送货后均要返回配货中心P，重新装货后再前往其他超市．设P到A的路程为xkm，这辆货车每天行驶的路程为ykm．

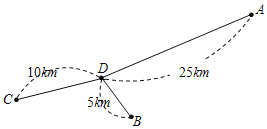
（1）求y与x之间的函数关系式，并写出自变量x的取值范围；

（2）直接写出配货中心P建在什么位置，这辆货车每天行驶的路程最短？最短路程是多少？

Answer 1

【答案】（1）y═-4x+180（2≤x≤23）；（2）当配货中心P建在AP=23km位置时，这辆货车每天行驶的路程最短．其最短路程是88km．

【解析】

1）由题意得2≤x≤25-2，结合图象分别得出货车从P到A，B，C，D的距离，进而得出y与x的函数关系；

（2）利用（1）中所求得出函数解析式，利用x的取值范围，根据函数的性质求得最小值及此时的x的值．

解：（1）∵由题意得2≤x≤25-2，

货车从P到A往返1次的路程为2x，

货车从P到B往返1次的路程为：2（5+25-x）=60-2x，

货车从P到C往返1次的路程为：2（25-x+10）=70-2x，

货车从P到D往返1次的路程为：2（25-x）=50-2x，

这辆货车每天行驶的路程为：y=2x+60-2x+70-2x+50-2x=-4x+180，

即；

（2）∵y═-4x+180（2≤x≤23），其中a=-4＜0，

∴y随x的增大而减小，

∴当x=23时，ymin=-4×23+180=88；

∴当配货中心P建在AP=23km位置时，这辆货车每天行驶的路程最短．其最短路程是88km．

故答案为：（1）y═-4x+180（2≤x≤23）；（2）当配货中心P建在AP=23km位置时，这辆货车每天行驶的路程最短．其最短路程是88km．