Question

【题目】矩形AOCD绕顶点A（0，5）逆时针方向旋转，当旋转到如图所示的位置时，边BE交边CD于M，且ME=2，CM=4．

（1）求AD的长；
（2）求阴影部分的面积和直线AM的解析式；
（3）求经过A、B、D三点的抛物线的解析式；
（4）在抛物线上是否存在点P，使S△PAM=？若存在，求出P点坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：作BP⊥AD于P，BQ⊥MC于Q，如图1，

∵矩形AOCD绕顶点A（0，5）逆时针方向旋转得到矩形ABEF，

∴AB=AO=5，BE=OC=AD，∠ABE=90°，

∵∠PBQ=90°，

∴∠ABP=∠MBQ，

∴Rt△ABP∽Rt△MBQ，

∴，

设BQ=PD=x，AP=y，则AD=x+y，BM=x+y﹣2，

∴，

∴PBMQ=xy，

∵PB﹣MQ=DQ﹣MQ=DM=1，

∴（PB﹣MQ）2=1，即PB2﹣2PBMQ+MQ2=1，

∴52﹣y2﹣2xy+（x+y﹣2）2﹣x2=1，解得x+y=7，

∴BM=5，

∴BE=BM+ME=5+2=7，

∴AD=7；

（2）

解：∵AB=BM，

∴Rt△ABP≌Rt△MBQ，

∴BQ=PD=7﹣AP，MQ=AP，

∵BQ2+MQ2=BM2，

∴（7﹣MQ）2+MQ2=52，解得MQ=4（舍去）或MQ=3，

∴BQ=7﹣3=4，

∴S阴影部分=S梯形ABQD﹣S△BQM

=×（4+7）×4﹣×4×3

=16；

设直线AM的解析式为y=kx+b，

把A（0，5），M（7，4）代入得，解得，

∴直线AM的解析式为y=﹣x+5；

（3）

解：设经过A、B、D三点的抛物线的解析式为y=ax2+bx+c，

∵AP=MQ=3，BP=DQ=4，

∴B（3，1），

而A（0，5），D（7，5），

∴，解得，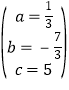

∴经过A、B、D三点的抛物线的解析式为y=x2﹣x+5；

（4）

解：当点P在线段AM的下方的抛物线上时，作PK∥y轴交AM于K，如图2

设P（x，﹣x+5），则K（x，﹣x+5），则KP=﹣+x，根据三角形面积公式可得到（﹣x2+x）7=，解得x1=3，x2=，于是得到此时P点坐标为（3，1）、（，）；再求出过点（3，1）与（，）的直线l的解析式为y=﹣x+，则可得到直线l与y轴的交点A′的坐标为（0，），所以AA′=，然后把直线AM向上平移个单位得到l′，直线l′与抛物线的交点即为P点，由于A″（0，），则直线l′的解析式为y=﹣x+，再通过解方程组得P点坐标为(3,1)、

（）、（）、（）．

【解析】

（1）作BP⊥AD于P，BQ⊥MC于Q，如图1，根据旋转的性质得AB=AO=5，BE=OC=AD，∠ABE=90°，利用等角的余角相等得∠ABP=∠MBQ，可证明Rt△ABP∽Rt△MBQ得到，设BQ=PD=x，AP=y，则AD=x+y，所以BM=x+y﹣2，利用比例性质得到PBMQ=xy，而PB﹣MQ=DQ﹣MQ=DM=1，利用完全平方公式和勾股定理得到52﹣y2﹣2xy+（x+y﹣2）2﹣x2=1，解得x+y=7，则BM=5，BE=BM+ME=7，所以AD=7；

（2）由AB=BM可判断Rt△ABP≌Rt△MBQ，则BQ=PD=7﹣AP，MQ=AP，利用勾股定理得到（7﹣MQ）2+MQ2=52，解得MQ=4（舍去）或MQ=3，则BQ=4，根据三角形面积公式和梯形面积公式，利用S阴影部分=S梯形ABQD﹣S△BQM进行计算即可；然后利用待定系数法求直线AM的解析式；

（3）先确定B（3，1），然后利用待定系数法求抛物线的解析式；

（4）当点P在线段AM的下方的抛物线上时，作PK∥y轴交AM于K，如图2设P（x，﹣x+5），则K（x，﹣x+5），则KP=﹣+x，根据三角形面积公式得到（﹣x2+x）7=，解得x1=3，x2=，于是得到此时P点坐标为（3，1）、（，）；再求出过点（3，1）与（，）的直线l的解析式为y=﹣x+，则可得到直线l与y轴的交点A′的坐标为（0，），所以AA′=，然后把直线AM向上平移个单位得到l′，直线l′与抛物线的交点即为P点，由于A″（0，），则直线l′的解析式为y=﹣x+，再通过解方程组得P点坐标．

【考点精析】本题主要考查了二次函数图象的平移的相关知识点，需要掌握平移步骤：（1）配方 y=a(x-h)2+k，确定顶点（h,k）（2）对x轴左加右减；对y轴上加下减才能正确解答此题．