题目内容
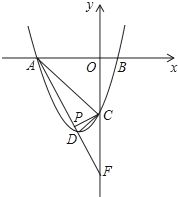
【题目】如图，已知抛物线y=ax2+bx+c与x轴交于点A、B，与直线AC：y=﹣x﹣6交y轴于点C，点D是抛物线的顶点，且横坐标为﹣2．
（1）求出抛物线的解析式．
（2）判断△ACD的形状，并说明理由．
（3）直线AD交y轴于点F，在线段AD上是否存在一点P，使∠ADC=∠PCF？若存在，直接写出点P的坐标；若不存在，说明理由．
【答案】
（1）
解：（1）由直线AC：y=﹣x﹣6，可得A（﹣6，0），C（0，﹣6），
∵抛物线y=ax2+bx+c与x轴交于点A、B，抛物线的顶点D的横坐标为﹣2，
∴B（2，0）．
把A、B、C三点坐标分别代入y=ax2+bx+c，得
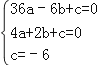，解得
，
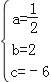∴抛物线的解析式为
；
（2）
解：△ACD是直角三角形，理由如下：
∵=
，
∴顶点D的坐标是（﹣2，﹣8）．
∵A（﹣6，0），C（0，﹣6），
∴AC2=62+62=72，CD2=22+（﹣8+6）2=8，AD2=（﹣2+6）2+82=80，
∴AC2+CD2=AD2，
∴△ACD是直角三角形，∠ACD=90°；
（3）
解：假设在线段AD上存在一点P，使∠ADC=∠PCF．
设直线AD的解析式为y=mx+n，
∵A（﹣6，0），D（﹣2，﹣8），
∴
，解得
，
∴直线AD的解析式为y=﹣2x﹣12，
∴F点坐标为（0，﹣12），设点P的坐标为（x，﹣2x﹣12）．
∵∠ADC=∠DCF+∠DFC，∠PCF=∠DCF+∠PCD，∠ADC=∠PCF，
∴∠DFC=∠PCD．
在△CPD与△FPC中，
，
∴△CPD∽△FPC，
∴
，
∴
=
，
整理得，35x2+216x+324=0，
解得x1=
，x2=
（舍去），
当x=时，﹣2x﹣12=﹣2×（）﹣12=
，
故所求点P的坐标为（，）．
【解析】（1）先由直线AC的解析式为y=﹣x﹣6，可得A（﹣6，0），C（0，﹣6），再根据抛物线的对称性求出B（2，0）．然后把A、B、C三点坐标分别代入y=ax2+bx+c，利用待定系数法即可求解；
（2）先求出抛物线顶点D的坐标，再根据两点间的距离公式计算得出AC2=62+62=72，CD2=22+（﹣8+6）2=8，AD2=（﹣2+6）2+82=80，那么AC2+CD2=AD2 ， 利用勾股定理的逆定理即可得到△ACD是直角三角形；
（3）先利用待定系数法求出直线AD的解析式为y=﹣2x﹣12，得到F（0，﹣12），设点P的坐标为（x，﹣2x﹣12）．由∠ADC=∠DCF+∠DFC，∠PCF=∠DCF+∠PCD，∠ADC=∠PCF，可得∠DFC=∠PCD．根据两角对应相等的两三角形相似证明△CPD∽△FPC，那么，依此列出比例式=，解方程求出x的值，进而得到点P的坐标．
