题目内容
【题目】如图,在四边形ABCD中,AB⊥BC,对角线AC、BD相交于点E,E为BD中点,且AD=BD,AB=2,∠BAC=30°,则DC=_____.

【答案】![]()
【解析】
如图,在EA上取一点K,使得EK=CE,连接DK,BK,延长DK交AB于H.首先证明四边形BCDK是平行四边形,再证明DH⊥AB,由DA=DB,推出AH=HB,AK=BK=CD即可解决问题;
如图,在EA上取一点K,使得EK=CE,连接DK,BK,延长DK交AB于H.
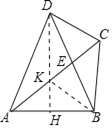
∵DE=EB,CE=EK,
∴四边形BCDK是平行四边形,
∴CD=BK,DK∥BC,
∵BC⊥AB,∴DH⊥AB,
∵DA=DB,∴AH=HB=1,
∴KA=KB=CD,
在Rt△AKH中,∠BAC=30°,
AK=AH÷cos30°=![]() ,
,
∴CD=![]() ,
,
故答案为![]() .
.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目