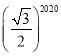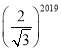题目内容
【题目】已知等边三角形的三条边相等，三个角都等于
，如图，
与
都是边三角形，连接
.
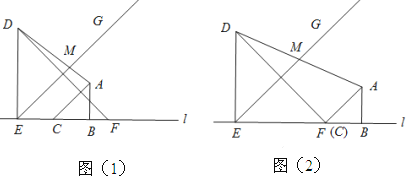
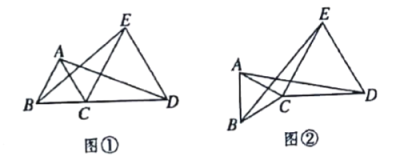
（1）如果点
在同一条直线上，如图①所示，试说明：
；
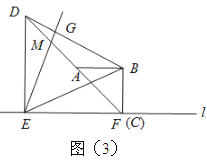
（2）如果绕
点转过一个角度，如图②所示，（1）中的结论还能否成立？请说明理由.
【答案】（1）见解析；（2）见解析.
【解析】
根据等边三角形的性质和角的和差，证明△ABC和△CDE全等，然后根据全等三角形的性质即可证明；
（2）按照（1）的思路进行证明即可.
证明：（1）∵
与
都是边三角形
∴BC=AC,CD=CE,∠BCA=∠ACD
∴∠BCA+∠ACE=∠ACD+∠ACE
∴∠BCE=∠ACD
在
与
中
∴≌（SAS）
∴AD=BE
(2)成立；理由如下：
（1）∵与都是边三角形
∴BC=AC,CD=CE,∠BCA=∠ACD
∴∠BCA+∠ACE=∠ACD+∠ACE
∴∠BCE=∠ACD
在与中
∴≌（SAS）
∴AD=BE
练习册系列答案
相关题目
