��Ŀ����
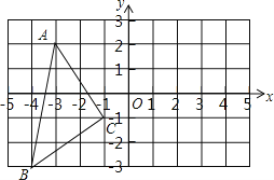
����Ŀ����֪����ƽ��ֱ������ϵxOy�У����κ���y��ax2��bx��3(a��0)��ͼ����x�ύ��A��B���㣬��A�ڵ�B����࣬��y�ύ�ڵ�C����OC��OB��3OA��
(1)��������κ����Ľ���ʽ��
(2)���D�ǵ�C���ڴ������߶Գ���ĶԳƵ㣬ֱ��AD��BC���ڵ�P�����ж�ֱ��AD��BC�Ƿ�ֱ����֤����Ľ��ۣ�
(3)��(2)�������£�����M��N�ֱ�������PC��PD�ϵĵ㣬�ʣ��Ƿ���������ĵ�M��N��ʹ���Ե�P��M��NΪ���������������ACPȫ��?�������������M��N�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�(1)y��x2��2x��3�� (2)AD��BC��(3)���ڣ�M1(1����2)��N1(4����3)����M2(0����3)��N2(3����2)��
�����������������
��1�����������������κ���y��ax2��bx��3(a��0)��ͼ����x�ύ��A��B���㣬��A�ڵ�B����࣬��y�ύ�ڵ�C����OC��OB��3OA���ɵõ�C��0��-3������A��-1,0������B��3,0������A��B���������������ʽ�����a��b��ֵ���Ϳɵõ�����ʽ�ˣ�
��2���ѣ�1�����������ʽ�䷽��Ϊ����ʽ���õ��Գ��᷽�̣��Ϳɵõ�D�����꣬����A��B��C��D�ĵ�������з���������ֱ��AD��ֱ��BC�Ľ���ʽ������������ʽ�С�k����ֵ�ij˻��Ƿ�Ϊ��-1���Ϳ��ж���ֱ���Ƿ�ֱ�ˣ�
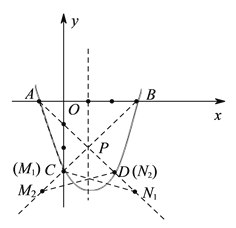
��3����ͼ���ɣ�2��������AD��BC�Ľ���ʽ���з�������P�����꣬������BC������AD���ഹֱ������Ϊ��P����֪��APC�͡�PMN����ֱ�������Σ�Ȼ�����������������ۣ�����PN=PA��M��C�غ�ʱ����APC���PMNȫ�ȣ�����PM=PA��N��D�غ�ʱ����APC���PMNȫ�ȣ��������Ӧ�ĵ�M��N������.
���������
��1�������κ���y��ax2��bx��3(a��0)��y�ύ�ڵ�C��
����C��������0��-3����
��OC=3��
����OC=OB=3OA��
��OB=3��OA=1��
�������κ���y��ax2��bx��3(a��0)��ͼ����x�ύ��A��B���㣬��A�ڵ�B����࣬
����A��B������ֱ�Ϊ��-1��0������3��0����
��A��B������������ʽy��ax2��bx��3(a��0)���� ![]() ����ã�
����ã� ![]() ��
��
����κ�������ʽΪ�� ![]() ��
��
��2����![]() ��֪���������ߵĶԳ���Ϊֱ����
��֪���������ߵĶԳ���Ϊֱ���� ![]() ��
��
����D�͵�C��0��-3������ֱ��![]() �Գ���
�Գ���
����D��������2��-3����
��ֱ��AD��ֱ��BC�Ľ���ʽ�ֱ�Ϊ�� ![]() ����A��B��C��D������ֱ������Ӧ�Ľ���ʽ�ã�
����A��B��C��D������ֱ������Ӧ�Ľ���ʽ�ã� ![]() ��
�� ![]() ��
��
����� ![]() ��
�� ![]() ��
��
��ֱ��AD�Ľ���ʽΪ�� ![]() ��ֱ��BC�Ľ���ʽΪ��
��ֱ��BC�Ľ���ʽΪ�� ![]() ��
��
��![]() ��
��
��ֱ��AD��ֱ��BC�ǻ��ഹֱ�ģ�
��3������ʹ��APC����PMNȫ�ȵĵ�M��N���������£�
�ɣ� ![]() ���
���![]() ��
��
���P��������1��-2����
����ͼ��������BC������AD���ഹֱ������Ϊ��P��
���APC���PMN����ֱ�������Σ�
���������������������������ȫ����
����M��C�غϣ�PN=PAʱ����������ȫ�ȣ���ʱM����Ϊ��0��-3�������߶��е����깫ʽ�ɵ�N������Ϊ��3��-4����
����N��D�غϣ�PM=PAʱ������������ȫ�ȣ���ʱN������Ϊ��2��-3�������������빫ʽ�����M������Ϊ��-1��-4����
�ۺ��٢���֪����M��N������Ϊ��
![]() ��
��![]() ʱ����APC���PMNȫ��.
ʱ����APC���PMNȫ��.

 ��У����ϵ�д�
��У����ϵ�д�