题目内容
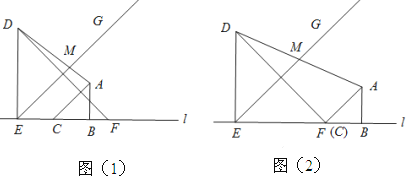
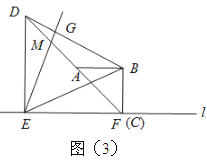
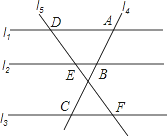
【题目】已知:如图,![]() 平分
平分![]() ,
,![]() ,垂足为
,垂足为![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,
,![]() 分别与线段
分别与线段![]() ,
,![]() 相交于
相交于![]() ,
,![]() .
.
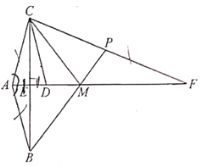
(1)求证:![]() ;
;
(2)若![]() ,请你判断
,请你判断![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(1)证明见解析 (2)答案见解析
【解析】
(1)由![]() ,BC⊥AD易证AC=CD,再根据角平分线及垂直得到∠ACE=∠ABE ,利用等角对等边证明AC=AB,可得结论AB=CD;
,BC⊥AD易证AC=CD,再根据角平分线及垂直得到∠ACE=∠ABE ,利用等角对等边证明AC=AB,可得结论AB=CD;
(2)易证∠CAD=∠CDA=∠MPC,则∠MPF=∠CDM,然后根据AM为BC的中垂线,可得∠CMA=∠BMA=PMF,可得到∠MCD=∠F.
(1)证明:∵AF平分∠BAC,
∴∠CAD=∠BAD,
∵![]() ,
,
∵BC⊥AD,
∴BC为AD的中垂线,
∴AC=CD.
在Rt△ACE和Rt△ABE中,∠CAD+∠ACE=∠BAD+∠ABE=90°,
∴∠ACE=∠ABE,
∴AC=AB,
∴AB=CD;
(2)解:∠MCD=∠F,
理由如下:∵∠BAC=2∠MPC,
又∵∠BAC=2∠CAD,
∴∠MPC=∠CAD,
∵AC=CD,
∴∠CAD=∠CDA,
∴∠MPC=∠CDA,
∴∠MPF=∠CDM,
∵AC=AB,AE⊥BC,
∴CE=BE,
∴AM为BC的中垂线,
∴CM=BM.
∵EM⊥BC,
∴EM平分∠CMB.
∴∠CME=∠BME,
∵∠BME=∠PMF,
∴∠PMF=∠CME,
∴∠MCD=∠F.

 发散思维新课堂系列答案
发散思维新课堂系列答案【题目】如图,是某广场台阶(结合轮椅专用坡道)景观设计的模型,以及该设计第一层的截面图,第一层有十级台阶,每级台阶的高为0.15米,宽为0.4米,轮椅专用坡道AB的顶端有一个宽2米的水平面BC;《城市道路与建筑物无障碍设计规范》第17条,新建轮椅专用坡道在不同坡度的情况下,坡道高度应符合以下表中的规定:
坡度 | 1:20 | 1:16 | 1:12 |
最大高度(米) | 1.50 | 1.00 | 0.75 |
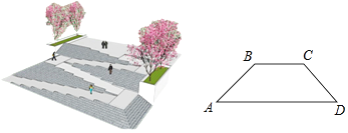
(1)选择哪个坡度建设轮椅专用坡道AB是符合要求的?说明理由;
(2)求斜坡底部点A与台阶底部点D的水平距离AD.