题目内容
【题目】已知二次函数y=x2+bx+c（b，c是常数）的图象经过点（1，﹣1）．
（1）用含b的代数式表示c．
（2）求二次函数图象的顶点纵坐标的最大值，并写出此时二次函数的表达式．
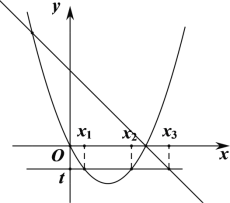
（3）垂直于y轴的直线与（2）中所得的二次函数图象交于（x1，y1）和（x2，y2），与一次函数y=﹣x+2的图象交于（x3，y3），若x1<x2<x3，求x1+x2+x3的取值范围．
【答案】（1）c=﹣b－2；（2）﹣1，此时y=x2－2x；（3）4<x1+x2+x3<5．
【解析】
（1）把点（1，﹣1）代入抛物线的解析式，整理即可得出结果；
（2）根据二次函数的顶点坐标公式和（1）题的结果可得抛物线顶点的纵坐标关于b的二次函数，再根据二次函数的性质即可求出其最大值，进而可得结果；
（3）设垂直于y轴的直线为y=t，则x1、x2是方程x2－2x=t的两个根，由此可得x1+x2的值，且只有当
时，满足x1<x2<x3，如图，由此可得关于x3的不等式组，解不等式组即可求出x3的取值范围，进而可得结果。
解：（1）∵二次函数y=x2+bx+c（b，c是常数）的图象经过点（1，﹣1），
∴﹣1=1+b+c，
∴c=﹣b－2；
（2）抛物线顶点的纵坐标=
，
∴当b=﹣2时，二次函数图象的顶点纵坐标的最大值是﹣1；
此时c=0，二次函数的解析式是：y=x2－2x；
（3）设垂直于y轴的直线为y=t，抛物线y=x2－2x=（x－1）2－1，
由题意可得：只有当时，满足x1<x2<x3，如图，
则x1、x2是方程x2－2x=t的两个根，即x2－2x－t=0，
∴x1+x2=2，
当时，
，解得：
，
∴4<x1+x2+x3<5．
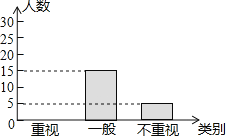
【题目】某教研机构为了了解初中生课外阅读名著的现状，随机抽取了某校50名初中生进行调查，依据相关数据绘制成了以下不完整的统计图，请根据图中信息解答下列问题：
类别 | 重视 | 一般 | 不重视 |
人数 | a | 15 | b |
（1）求表格中a，b的值；
（2）请补全统计图；
（3）若某校共有初中生2000名，请估计该校“重视课外阅读名著”的初中生人数．
