题目内容
【题目】在直角坐标系中，直线
与
轴交于点
，按如图方式作正方形
、
、
，点
、
、
在直线上，点
、
、
在
轴上，图中阴影部分三角形的面积从左到右依次记为
、
、
、
，则
的值为__________．
【答案】
【解析】
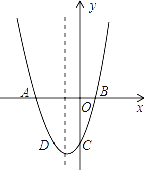
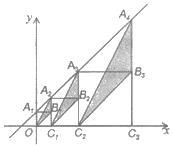
结合正方形的性质结合直线的解析式可得出：A2B1=OC1，A3B2=C1C2，A4B3=C2C3，…，结合三角形的面积公式即可得出：S1=
OC12=，S2=C1C22=2，S3=
C2C32=8，…，根据面积的变化可找出变化规律“Sn=22n-3（n为正整数）”，依此规律即可得出结论．
解：令一次函数y=x+1中x=0，则y=1，
∴点A1的坐标为（0，1），OA1=1．
∵四边形AnBnCnCn-1（n为正整数）均为正方形，
∴A1B1=OC1=1，A2B2=C1C2=2，A3B3=C2C3=4，…．
令一次函数y=x+1中x=1，则y=2，
即A2C1=2，
∴A2B1=A2C1-A1B1=1=A1B1，
∴tan∠A2A1B1=1．
∵AnCn-1⊥x轴，
∴tan∠An+1AnBn=1．
∴A2B1=OC1，A3B2=C1C2，A4B3=C2C3，…．
∴S1=OC12=，S2=C1C22=2，S3=C2C32=8，…，
∴Sn=22n-3（n为正整数），∴
=
=.
【题目】下表中给出
，
，
三种手机通话的收费方式．
收费方式 | 月通话费/元 | 包时通话时间/ | 超时费/（元/ |
|
|
|
|
|
|
|
|
|
| 不限时 |
（1）设月通话时间为
小时，则方案，，的收费金额
，
，
都是的函数，请分别求出这三个函数解析式．
（2）填空：
若选择方式最省钱，则月通话时间的取值范围为______；
若选择方式最省钱，则月通话时间的取值范围为______；
若选择方式最省钱，则月通话时间的取值范围为______；
（3）小王、小张今年
月份通话费均为
元，但小王比小张通话时间长，求小王该月的通话时间．
