��Ŀ����
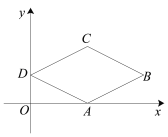
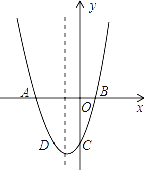
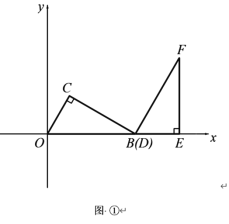
����Ŀ����ƽ��ֱ������ϵ�У�������״����С��ȫ��ͬ�����ǰ�OBC��DEF������ͼ��ʾ��λ�ðڷţ�OΪԭ�㣬��B(12��0) ����B���D�غϣ���OB���DE����x���ϣ����У���C=��DEF=90������OBC=��F=30����
��1����ͼ�������C���ꣻ
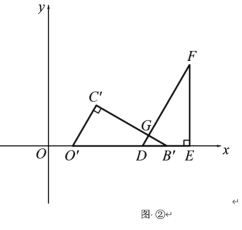
��2���̶ֹ����ǰ�DEF�������ǰ�OBC��x��������ƽ�ƣ��õ���O��B��C�� ������O�� ���D��ʱֹͣ�˶��������ǰ�ƽ�Ƶľ���Ϊx���������ǰ��ص����ֵ����Ϊy����y����x�ĺ�������ʽ����д���Ա���x��ȡֵ��Χ��
��3���ڣ�2�������£����BC���е�Ϊ��M����DF���е�Ϊ��N��ֱ��д�������ǰ�ƽ�ƹ����У�����M���N֮��ľ�����Сʱ����M�����ֱ꣨��д��������ɣ���
���𰸡���1��C (3 ,![]() )����2��
)����2�� ����3��M
����3��M ![]()
��������
��1������C��CG��AB��G�㣬����B(12��0) ����C=��DEF=90������OBC=��F=30������OB=12�� OC=6������OG=OCcos60����CG=OCsin60�����������ɵõ����ꣻ
��2���������ۣ��ٵ�![]() ʱ���ڵ�
ʱ���ڵ�![]() ʱ�����������ε������ʽ���г����̿ɵô𰸣�
ʱ�����������ε������ʽ���г����̿ɵô𰸣�
��3�����ݵ���ֱ�������е�������д��߶���̣���![]() ��
��![]() ��ʱ
��ʱ![]() ��̣����������ε���λ�ߣ��ɵ�
��̣����������ε���λ�ߣ��ɵ�![]() ��
��![]() �ij��������߶εĺͲ�ɵõ�M�����꣮
�ij��������߶εĺͲ�ɵõ�M�����꣮
�⣺��1����ͼ����ʾ������C��CG��AB��G�㣮
��B(12��0) ����OB=12��
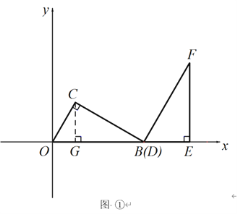
��Rt��OBC����OB=12����OBC=30������OC=6��
���COB=60��
��Rt��OCG��OG=OCcos60��=3��
��CG=OCsin60��=![]() ��
��
��C (3 ,![]() ).
).
��2������0��x��6ʱ����ͼ����ʾ��
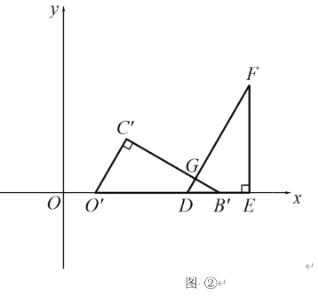
��GDE=60������GB��D=30����DB��=x����
DG=![]() ��B��G=
��B��G=![]() ���ص����ֵ����Ϊ
���ص����ֵ����Ϊ
y=![]() DGB��G=
DGB��G=![]()
![]() x
x![]()
����6��x��12ʱ����ͼ����ʾ��

B��D=x��DG=![]() x��B��G=
x��B��G=![]() ��B��E=x��6��
��B��E=x��6��
EH=![]() ��
��
�ص����ֵ����Ϊy=S��B��DG��S��B��EH=![]() DGB��G��
DGB��G��![]() B��EEH��
B��EEH��
��y=![]()
![]() x
x![]() -
-![]()
![]()
![]()
����y=![]() ��
��
���������� ��
��
��3����ͼ5��ʾ����![]() ��
��![]() �㣬
�㣬
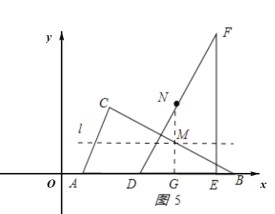
��![]() ��
��![]() ��ʱ
��ʱ![]() ��̣�
��̣�
��![]() ��
��![]() ����λ�ߣ�
����λ�ߣ�
��![]() ��
��![]() ��
��
��![]() ��
��
��M��������![]() ��
��