题目内容
如图,正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是


| A.点P | B.点Q | C.点R | D.点M |
B
根据垂径定理的推论“弦的垂直平分线必过圆心”,作两条弦的垂直平分线,交点即为圆心.
解:根据垂径定理的推论,则
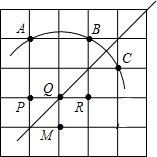
作弦AB和BC的垂直平分线,交点Q即为圆心.
故选B.
点评:此题主要是垂径定理的推论的运用.
解:根据垂径定理的推论,则

作弦AB和BC的垂直平分线,交点Q即为圆心.
故选B.
点评:此题主要是垂径定理的推论的运用.

练习册系列答案
相关题目
 所在圆的圆心,∠AOC=108°,点D在AB的延长线上, BD=BC, 则∠D的度数为( )
所在圆的圆心,∠AOC=108°,点D在AB的延长线上, BD=BC, 则∠D的度数为( )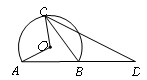
 ,若过点
,若过点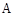 、点
、点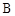 作圆,那么下面说法正确的是( )
作圆,那么下面说法正确的是( ) 不在该圆的外部,就在该圆的内部
不在该圆的外部,就在该圆的内部 的中垂线上
的中垂线上 则图中三个扇形(阴影部分)的面积之和是 cm2.
则图中三个扇形(阴影部分)的面积之和是 cm2. 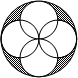
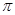
 -4
-4
