题目内容
如图，已知⊙O是△ABC的内切圆，切点为D、E、F，如果AE=2，CD=1，BF=3，则内切圆的半径r ．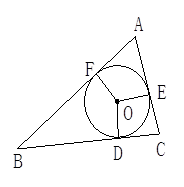
1
根据切线长定理得出AF=AE，EC=CD，DB=BF，进而得出△ABC是直角三角形，再利用直角三角形内切圆半径求法得出内切圆半径即可．
解：∵⊙O是△ABC的内切圆，切点为D、E、F，
∴AF=AE，EC=CD，DB=BF，
∵AE=2，CD=1，BF=3，
∴AF=2，EC=1，BD=3，
∴AB=BF+AF=3+2=5，BC=BD+DC=4，AC=AE+EC=3，
∴△ABC是直角三角形，
∴内切圆的半径r=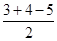
=1，
故答案为：1．
解：∵⊙O是△ABC的内切圆，切点为D、E、F，
∴AF=AE，EC=CD，DB=BF，
∵AE=2，CD=1，BF=3，
∴AF=2，EC=1，BD=3，
∴AB=BF+AF=3+2=5，BC=BD+DC=4，AC=AE+EC=3，
∴△ABC是直角三角形，
∴内切圆的半径r=
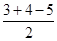=1，故答案为：1．
练习册系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目
和⊙
的半径分别是12和2，圆心
。”那么，据此你判断儿子打球所用的时间应是（）
，求BC的长．
