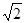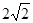题目内容
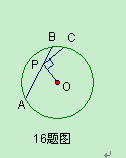
如图，点O为优弧
所在圆的圆心，∠AOC=108°，点D在AB的延长线上, BD=BC, 则∠D的度数为（ ）
所在圆的圆心，∠AOC=108°，点D在AB的延长线上, BD=BC, 则∠D的度数为（ ）| A．20° | B．27° |
| C．30° | D．54° |
B
先根据圆周角定理可得∠ABC=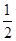
∠AOC，易求∠ABC，而BC=BD，易得∠BCD=∠D，且∠ABC是△BCD的外角，从而易得∠ABC=2∠D，进而可求∠D．
解：∵∠AOC、∠ABC是同弧对的圆心角和圆周角，
∴∠AB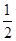C=∠AOC，
∵∠AOC=108°，
∴∠ABC=54°，
∵∠ABC是△ABD的外角，
∴∠ABC=∠BCD+∠D，
∵BD=BC，
∴∠BCD=∠D，
∴∠ABC=∠BCD+∠D=2∠D，
∴∠D=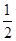∠ABC=27°．
故选B．
本题考查了圆周角定理、等腰三角形的性质、三角形的外角性质．解题的关键是先求出∠ABC．
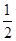∠AOC，易求∠ABC，而BC=BD，易得∠BCD=∠D，且∠ABC是△BCD的外角，从而易得∠ABC=2∠D，进而可求∠D．解：∵∠AOC、∠ABC是同弧对的圆心角和圆周角，
∴∠ABC=
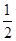∠AOC，∵∠AOC=108°，
∴∠ABC=54°，
∵∠ABC是△ABD的外角，
∴∠ABC=∠BCD+∠D，
∵BD=BC，
∴∠BCD=∠D，
∴∠ABC=∠BCD+∠D=2∠D，
∴∠D=
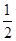∠ABC=27°．故选B．
本题考查了圆周角定理、等腰三角形的性质、三角形的外角性质．解题的关键是先求出∠ABC．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
、
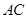是
的两条弦，
=30°，过点
的切线与
的延长线交于点
，则
的度数为 ．
为半径的圆在运动过程中与△ABC的边第二次相切时是点O出发后第______秒．
OP，PC交⊙O，若AP＝4，PB＝2，则PC的长是 （ ）
