Question

【题目】如图，在△ABC中，∠B=90°，点B、C、D在同一直线上，△ABC≌△CDE，且∠B=∠D，∠BAC=∠DCE.

（1）试说明BD=AB+ED；

（2）若∠CED=2∠BAC，求∠CED的度数；

（3）连接AE，则△ACE是怎样的三角形？说明理由.

Answer 1

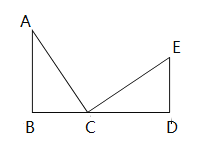
【答案】（1）详见解析；（2）60°；（3）△ACE是等腰直角三角形，理由详见解析.

【解析】

（1）根据全等三角形的性质即可求解；

（2）根据全等三角形的性质得到∠ACB=∠CED，再根据直角三角形的性质得到∠BAC+∠ACB=90°，根据已知条件∠CED=2∠BAC，可求出∠BAC=30°，即可得到∠CED=60°.

（3）根据全等三角形的性质即可得到AC⊥CE，AC=CE，故可求解.

（1）∵ △ABC≌△CDE，

∴ AB=CD，BC=DE.

∴ AB+ED=BC+CD=BD. 即BD=AB+ED.

（2）∵ △ABC≌△CDE，

∴ ∠ACB=∠CED.

在△ABC中，∠B=90°，

∴ ∠BAC+∠ACB=90°.

∵ ∠CED=2∠BAC，

∴ 3∠BAC=90°，

∴ ∠BAC=30°，

∴ ∠CED=60°.

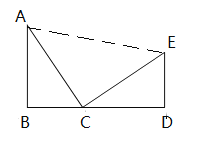
（3）△ACE是等腰直角三角形.

∵ ∠ACD是△ABC的一个外角，

∴ ∠ACD=∠BAC+∠B，即∠ACE+∠DCE=∠BAC+∠B.

∵ ∠BAC=∠DCE，∠B=90°，

∴ ∠ACE=90°.

∵ △ABC≌△CDE，

∴ AC=CE，

∴ △ACE是等腰直角三角形.