Question

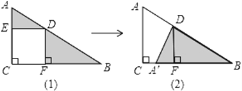
【题目】如图△ABC中有正方形EDFC，由图（1）通过三角形的旋转变换可以得到图（2）．观察图形的变换方式，若AD=3，DB=4，则图（1）中△ADE和△BDF面积之和S为_____．正方形EDFC的面积为_______

Answer 1

【答案】6；

【解析】

由图形可知△DA′F是由△DAE旋转得到，利用旋转的性质可得到△A′DB为直角三角形，可求得S，在Rt△A′DB中 由勾股定理可求得A′B，再利用面积相等可求得DF，可求得正方形EDFC的面积．

解：由旋转的性质得AD=A′D=3，∠ADE=∠A′DF，
∵∠A′DB=∠A′DF+∠FDB=∠ADE+∠FDB=90°，
∴在Rt△A′DB中，
S△A′DB=A′D×BD=×3×4=6，
∴S△ADE+S△BDF=S△A′DF+S△BDF=S△A′DB=6，
又A′D=3，BD=4，可求得A′B=5，
∴A′BDF=×5×DF=6，
∴DF=，
∴S正方形EDFC=DF2=，
故答案为：6；．