题目内容
【题目】如图，直线AB∥CD，直线l与直线AB、CD相交于点E、F，P是射线EA上的一个动点（不包括端点E），将△EFP沿PF折叠，便顶点E落在点Q处．若∠PEF＝54°，且∠CFQ＝
∠CFP，则∠PFE的度数是_____．
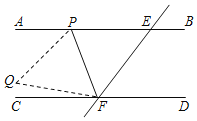
【答案】54°．
【解析】
依据平行线的性质，即可得到∠EFC的度数，再求出∠CFQ，即可求出∠PFE的度数．
∵AB∥CD，∠PEF＝54°，
∴∠PEF+∠EFC＝180°，
∴∠EFC＝180°﹣54°＝126°，
∵将△EFP沿PF折叠，便顶点E落在点Q处，
∴∠PFE＝∠PFQ，
∵∠CFQ＝
∠CFP，
∴∠CFQ＝
∠EFC＝×126°＝18°，
∴∠PFE＝
∠EFQ＝（∠EFC﹣∠CFQ）＝（126°﹣18°）＝54°．
故答案为：54°．
练习册系列答案
相关题目
