题目内容
【题目】如图,已知直线y=ax+b与双曲线y= ![]() (x>0)在第一象限内交于A(x1 , y1),B(x2 , y2)两点,与x轴交于点C(x0 , 0)
(x>0)在第一象限内交于A(x1 , y1),B(x2 , y2)两点,与x轴交于点C(x0 , 0)
(1)若A(2,2)、B(4,n) ①求直线和双曲线解析式
②直接写出S△AOB= ![]()
(2)直接写出x1、x2、x0之间的数量关系. 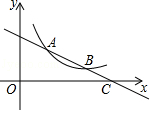
【答案】
(1)解:①∵直线y=ax+b与双曲线y= ![]() (x>0)在第一象限内交于A(x1,y1),B(x2,y2)两点,A(2,2)、B(4,n),
(x>0)在第一象限内交于A(x1,y1),B(x2,y2)两点,A(2,2)、B(4,n),
∴k=2×2=4,
∴双曲线解析式为y= ![]() ,
,
∴n= ![]() =1,
=1,
∴B(4,1),
把A(2,2)、B(4,1)代入直线y=ax+b得: ![]() ,
,
解得: 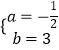 ,
,
∴直线解析式为y=﹣ ![]() x+3;
x+3;
②S△AOB=3.
(2)解:x1+x2=x0.理由如下:
由 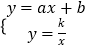 消去y得:ax2+bx﹣k=0,
消去y得:ax2+bx﹣k=0,
∵直线y=ax+b与双曲线y= ![]() (ak≠0)的两个交点的横坐标为x1、x2,
(ak≠0)的两个交点的横坐标为x1、x2,
∴x1+x2=﹣ ![]() ,
,
直线y=ax+b与x轴的交点为(﹣ ![]() ,0),
,0),
∴x0=﹣ ![]() ,
,
∴x1+x2=x0.
【解析】解:(1)②∵y=﹣ ![]() x+3,当y=0时,x=6;当x=0时,y=3, ∴C(6,0),
x+3,当y=0时,x=6;当x=0时,y=3, ∴C(6,0),
∴OC=6,
∴S△AOB= ![]() ×6×3﹣
×6×3﹣ ![]() ×3×2﹣
×3×2﹣ ![]() ×6×1=3;
×6×1=3;
所以答案是:3;

 名校课堂系列答案
名校课堂系列答案【题目】中国最大的水果公司“佳沃鑫荣懋”旗下子公司“欢乐果园”购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为P= 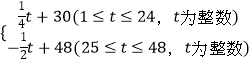 ,且其日销售量y(kg)与时间t(天)的关系如表:
,且其日销售量y(kg)与时间t(天)的关系如表:
时间t(天) | 1 | 3 | 6 | 10 | 20 | 40 | … |
日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | … |
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售前24天中,子公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
学生最喜欢的活动项目的人数统计表
项目 | 学生数(名) | 百分比 |
丢沙包 | 20 | 10% |
打篮球 | 60 | p% |
跳大绳 | n | 40% |
踢毽球 | 40 | 20% |
根据图表中提供的信息,解答下列问题: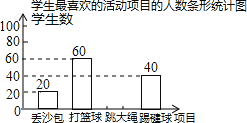
(1)m= , n= , p=;
(2)请根据以上信息直接补全条形统计图;
(3)根据抽样调查结果,请你估计该校2000名学生中有多少名学生最喜欢跳大绳.