题目内容
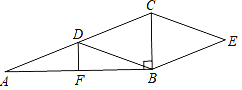
【题目】如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC,AD=3,DF=1,四边形DBEC面积是_____
【答案】4![]()
【解析】
根据平行四边形的判定定理首先推知四边形DBEC为平行四边形,然后由直角三角形斜边上的中线等于斜边的一半得到其邻边相等:CD=BD,得出四边形DBEC是菱形,由三角形中位线定理和勾股定理求得AB边的长度,然后根据菱形的性质和三角形的面积公式进行解答.
∵CE∥DB,BE∥DC,
∴四边形DBEC为平行四边形.
又∵Rt△ABC中,∠ABC=90°,点D是AC的中点,
∴CD=BD=![]() AC,
AC,
∴平行四边形DBEC是菱形;
∵点D,F分别是AC,AB的中点,AD=3,DF=1,
∴DF是△ABC的中位线,AC=2AD=6,S△BCD=![]() S△ABC,
S△ABC,
∴BC=2DF=2.
又∵∠ABC=90°,
∴AB=![]() =
=![]() .
.
∵平行四边形DBEC是菱形,
∴S四边形DBEC=2S△BCD=S△ABC=![]() ABBC=
ABBC=![]() ×4
×4![]() ×2=4
×2=4![]() ,
,
故答案为:4![]() .
.

练习册系列答案
相关题目