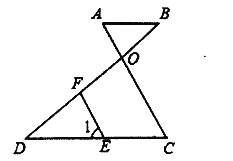
题目内容
【题目】在△ABC中,∠A![]() 90°,AB
90°,AB![]() AC.
AC.
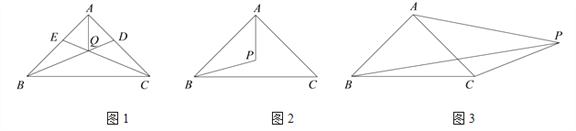
(1)如图1,△ABC的角平分线BD,CE交于点Q,请判断“![]() ”是否正确:________(填“是”或“否”);
”是否正确:________(填“是”或“否”);
(2)点P是△ABC所在平面内的一点,连接PA,PB,且PB![]()
![]() PA.
PA.
①如图2,点P在△ABC内,∠ABP![]() 30°,求∠PAB的大小;
30°,求∠PAB的大小;
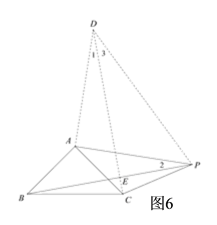
②如图3,点P在△ABC外,连接PC,设∠APC![]() α,∠BPC
α,∠BPC![]() β,用等式表示α,β之间的数量关系,并证明你的结论.
β,用等式表示α,β之间的数量关系,并证明你的结论.
【答案】(1)否;(2)①45°;②![]() .
.
【解析】试题分析:
(1)如图4,把△AQC顺时针旋转90°得到△AQ1B,连接QQ1,则由题意易得QQ1=![]() AQ,由已知条件可证∠BQ1Q
AQ,由已知条件可证∠BQ1Q![]() ∠Q1BQ,从而可得BQ
∠Q1BQ,从而可得BQ![]() QQ1=
QQ1=![]() AQ;
AQ;
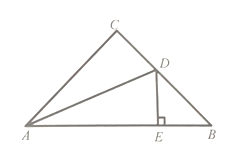
(2)①如图5,过点PD⊥AB于点,结合∠ABP=30°可得PD=![]() PB,结合PB=
PB,结合PB=![]() PA可得PD=
PA可得PD=![]() PA,由此即可得到sin∠PAB=
PA,由此即可得到sin∠PAB=![]() ,结合∠PAB是锐角即可得到∠PAB=45°;
,结合∠PAB是锐角即可得到∠PAB=45°;
②如图6,把△ABP绕点A逆时针旋转90°得到△ACD,连接DC,DP,则由旋转的性质可得: ∠1=∠2,PB=CD,∠DAP=90°,AD=AP,由此可得PD=![]() PA,结合PB=
PA,结合PB=![]() PA可证得PD=DC,从而得到∠PCD=∠CPD=45°+α,由此可得∠3=180°-2∠CPD=90°-2α,结合∠1=∠2=
PA可证得PD=DC,从而得到∠PCD=∠CPD=45°+α,由此可得∠3=180°-2∠CPD=90°-2α,结合∠1=∠2= ![]() ,可得∠1+∠3=90°-
,可得∠1+∠3=90°- ![]() =∠ADP=45°,变形即可得到:
=∠ADP=45°,变形即可得到: ![]() .
.
试题解析:
(1)如图4,把△AQC绕点A顺时针旋转90°得到△AQ1B,连接QQ1,
由旋转的性质可得:AQ1=AQ,∠Q1AQ=90°,
∴QQ1=![]() AQ,
AQ,
∵BQ、CQ分别平分∠ABC、∠ACB,
∴AQ平分∠BAC,
∴∠AQ1C=∠AQC=112.5°,
∴∠BQ1Q=112.5°-45°=67.5°,
∵∠Q1BQ=45°,
∴∠Q1BQ![]() ∠BQ1Q,
∠BQ1Q,
∴BQ![]() Q1Q=
Q1Q=![]() AQ.
AQ.
故答案为:“否”;
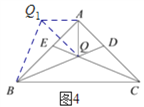
(2)① 如图5,作PD⊥AB于D,则∠PDB=∠PDA=90°,

∵ ∠ABP=30°,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
又∵∠PAB是锐角,
∴∠PAB=45°.
②![]() ,理由如下:
,理由如下:
如图6,把△ABP绕点A逆时针旋转90°得到△ACD,连接DC,DP,则由旋转的性质可得: ∠1=∠2,PB=CD,∠DAP=90°,AD=AP,
∴![]() ,∠ADP=∠APD=45°.
,∠ADP=∠APD=45°.
又∵![]() ,
,
∴ PD=PB=CD.
∴ ∠DCP=∠DPC.
∵ ∠APC![]() α,∠BPC
α,∠BPC![]() β,
β,
∴![]() ,
, ![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.