题目内容
【题目】已知二次函数![]() .
.
(1)该二次函数图象的对称轴是x![]() ;
;
(2)若该二次函数的图象开口向下,当![]() 时,
时, ![]() 的最大值是2,求当
的最大值是2,求当![]() 时,
时, ![]() 的最小值;
的最小值;
(3)若对于该抛物线上的两点![]() ,
, ![]() ,当
,当![]() ,
, ![]() 时,均满足
时,均满足![]() ,请结合图象,直接写出
,请结合图象,直接写出![]() 的最大值.
的最大值.
【答案】(1)2;(2)-6;(3)4.
【解析】试题分析:
(1)由二次函数![]() 的对称轴为直线
的对称轴为直线![]() 即可求出
即可求出![]() 的对称轴为直线:
的对称轴为直线: ![]() ;
;
(2)由题意结合(1)中所得抛物线的对称轴为直线![]() 可得,当
可得,当![]() 时,
时, ![]() 最大=
最大=![]() ,由此可解得
,由此可解得![]() ;由对称轴
;由对称轴![]() 把
把![]() 分为
分为![]() 和
和 ![]() 两个部分,结合对称轴两侧函数的增减性即可求得当
两个部分,结合对称轴两侧函数的增减性即可求得当![]() 时,
时, ![]() 的最小值;
的最小值;
(3)由题意可得抛物线![]() 和x轴交于点(1,0)和(3,0);分a>0和a<0两种情况画出图象结合已知条件进行分析解答即可;
和x轴交于点(1,0)和(3,0);分a>0和a<0两种情况画出图象结合已知条件进行分析解答即可;
试题解析:
(1)∵二次函数![]() 图象的对称轴为直线
图象的对称轴为直线![]() ,
,
∴二次函数![]() 的图象的对称轴为直线:
的图象的对称轴为直线: ![]() ;
;
(2)∵ 该二次函数的图象开口向下,且对称轴为直线![]() ,
,
∴ 当![]() 时,y取到在
时,y取到在![]() 上的最大值为2.
上的最大值为2.
∴![]() .
.
∴![]() ,
, ![]() .
.
∵ 当![]() 时,y随x的增大而增大,
时,y随x的增大而增大,
∴ 当![]() 时,y取到在
时,y取到在![]() 上的最小值
上的最小值![]() .
.
∵ 当![]() 时,y随x的增大而减小,
时,y随x的增大而减小,
∴ 当![]() 时,y取到在
时,y取到在![]() 上的最小值
上的最小值![]() .
.
∴ 当![]() 时,y的最小值为
时,y的最小值为![]() .
.
(3)∵二次函数![]() ,
,
∴二次函数的图象交![]() 轴于点(1,0)和(3,0),由此分
轴于点(1,0)和(3,0),由此分![]() 和
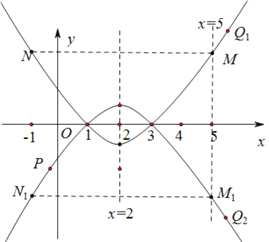
和![]() 画出图象如下:
画出图象如下:
①如图,当![]() 时,抛物线开口向上,由题意可知,此时点Q在直线
时,抛物线开口向上,由题意可知,此时点Q在直线![]() 的右侧,由图可知,此时不存t的值,使当
的右侧,由图可知,此时不存t的值,使当![]() ,
, ![]() 时,始终满足
时,始终满足![]() 成立;
成立;
②当![]() 时,抛物线开口向下,由题意可知,此时点Q在直线
时,抛物线开口向下,由题意可知,此时点Q在直线![]() 的右侧,由图可知,当点P在抛物线上点M和点N之间的部分图象上时,存在t,使当
的右侧,由图可知,当点P在抛物线上点M和点N之间的部分图象上时,存在t,使当![]() ,
, ![]() 时,始终满足
时,始终满足![]() 成立;此时,点M1关于抛物线对称轴
成立;此时,点M1关于抛物线对称轴![]() 的对称点N的横坐标为:-1,故
的对称点N的横坐标为:-1,故![]() ,解得
,解得![]() ,所以
,所以![]() 的最大值为
的最大值为![]() .
.
综合①②可得,满足条件的![]() 的最大值为
的最大值为![]() .
.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元) | 2 |
种植树木利润y1(万元) | 4 |
种植花卉利润y2(万元) | 2 |
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.






