题目内容
【题目】如图,直线![]() 与⊙O相切于点D,过圆心O作EF∥
与⊙O相切于点D,过圆心O作EF∥![]() 交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线
交⊙O于E、F两点,点A是⊙O上一点,连接AE,AF,并分别延长交直线![]() 于B、C两点;
于B、C两点;
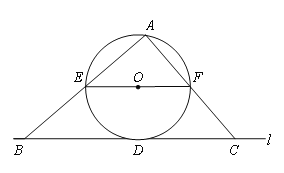
(1)求证:∠ABC+∠ACB=90°;
(2)若⊙O的半径![]() ,BD=12,求tan∠ACB的值.
,BD=12,求tan∠ACB的值.
【答案】(1)详见解析(2)tan∠ACB![]()
【解析】
(1)由直径所对圆周角是直角的性质和三角形内角和定理可得结论。
(2)求出tan∠BEH=![]() ,由∠ACB=∠BEH可得结论。
,由∠ACB=∠BEH可得结论。
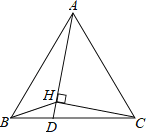
解(1)证明:如图,∵EF是⊙O的直径,∴∠EAF=90°。∴∠ABC+∠ACB=90°。
(2)连接OD,则OD⊥BD,过点E作EH⊥BC,垂足为点H,
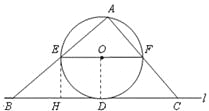
∴ EH∥OD。
∵EF∥BC,EH∥OD, OE=OD,
∴四边形EODH是正方形 。∴EH=HD=OD=5。
∵BD=12,∴BH=7。
在Rt△BEH中,tan∠BEH=![]() 。
。
又∵∠ABC+∠BEH=90°,∠ABC+∠ACB=90°,
∴∠ACB=∠BEH。∴tan∠ACB![]() 。
。

练习册系列答案
相关题目