题目内容
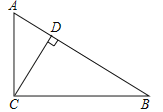
【题目】如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,
(1)尺规作图:作△ABC的角平分线AE,交CD于点F(不写作法,保留作图痕迹);
(2)求证:△CEF为等腰三角形.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)以A为圆心,任意长为半径画弧交AC、AB于M、N,分别以M、N为圆心大于![]() MN长为半径画弧,两弧交于点P,直线射线AP交BC于E,线段AE即为所求;4
MN长为半径画弧,两弧交于点P,直线射线AP交BC于E,线段AE即为所求;4
(2)只要证明∠CEF=∠CFE,即可推出CE=CF;
(1)如图线段AE即为所求;

(2)证明:∵CD⊥AB,
∴∠BDC=∠ACB=90°,
∴∠ACD+∠DCB=90°,∠DCB+∠B=90°,
∴∠ACD=∠B,
∵∠CFE=∠ACF+∠CAF,∠CEF=∠B+∠EAB,∠CAF=∠EAB,
∴∠CEF=∠CFE,
∴CE=CF,
∴△CEF是等腰三角形.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目