题目内容
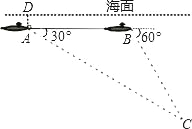
【题目】如图，在A处有一艘潜艇，并测得在俯视角为30°的方向有黑匣子，此时潜艇距海平面500米，继续在同一深度沿直线航行3000米后再次在B点出测得俯视角为60°正前方的海底黑匣子，求海底黑匣子所处位置C点出距离海面的深度．（保留根号）
【答案】点C距离海面的深度为（1500
+500）m．
【解析】
作CE⊥AB，交AB的延长线于点E，如图所示，设CE=x米，分别在直角三角形ACE与直角三角形BCE中，求出x的值，即可确定出所求．
作CE⊥AB，交AB的延长线于点E，如图所示，
设CE=x米，
在Rt△ACE中，∠A=30°，
∴AE=x，
在Rt△BEC中，∠EBC=60°，
∴BE=
x，
∵AE=AB+EB，
∴3000+x=x，
解得：x=1500，
则点C距离海面的深度为（1500+500）m．
练习册系列答案
相关题目
【题目】小冬与小夏是某中学篮球队的队员，在最近五场球赛中的得分如下表所示：
第一场 | 第二场 | 第三场 | 第四场 | 第五场 | |
小冬 | 10 | 13 | 9 | 8 | 10 |
小夏 | 12 | 2 | 13 | 21 | 2 |
（1）根据上表所给的数据，填写下表：
平均数 | 中位数 | 众数 | 方差 | |
小冬 | 10 | 10 | 2．8 | |
小夏 | 10 | 12 | 32．4 |
（2）根据以上信息，若教练选择小冬参加下一场比赛，教练的理由是什么？
（3）若小冬的下一场球赛得分是11分，则在小冬得分的四个统计量中（平均数、中位数、众数与方差）哪些发生了改变，改变后是变大还是变小？（只要回答是“变大”或“变小”）
（
）
